서 론
지표 미고결층의 불포화대는 강우가 지하로 침투하는 첫 번째 구간으로서 미고결층의 수리지질 특성에 의해서 침투속도가 결정된다. 지금까지 지표 미고결층의 물리적, 화학적, 생물학적 특성에 관한 연구들이 많이 수행되어왔다(Richards, 1931; USBR, 1977; Brooks and Corey, 1964; Lisk, 1972; Van Genuchten, 1980; Tiessen et al., 1994; Anderson, 2003; Lemenih et al., 2005; Ryu et al., 2008; Doussan and Ruy, 2009; Koch et al, 2011; Kim et al., 2014; Moret-Fernández and Latorre, 2017). 특히, 불포화대 매질의 토양 구조와 수리적 특성과의 관계와 같은 수리지질학적 특성에 대한 많은 연구가 이루어졌다(Richards, 1931; USBR, 1977; Brooks and Corey, 1964; Van Genuchten, 1980; Ryu et al., 2008; Moret-Fernández, Latorre, 2017; Wang et al., 2019). 한편, 균열암반의 포화대에 대한 수리적 특성에 대해서는 과거부터 많은 연구들이 수행되었으나(Hamm et al., 2007; Mejías et al., 2009; Chen et al., 2015), 균열암반의 불포화대에 대한 수리지질학적 특성 연구는 적은 편이다(Frohlich et al., 1996).
불포화대내에서 수직적인 물의 이동은 Richards(1931) 식에 의해서 표현된다. 불포화 수리전도도는 함수비에 따라 달라지며, 수두는 위치수두와 모세관 수두의 합이다. Van Genuchten(1980)은 토양층에서의 불포화 수리전도도와 토양수의 압력수두 및 함수비의 관계식을 제안하고, 제안된 식과 현장에서 구한 수리전도도를 서로 비교 ‧ 분석하였다. 수리전도도는 높은 변동계수를 가지며, 변동계수는 표준편차를 평균값으로 나눈 값으로써 변동의 크기를 나타낸다(Warrick and Nielsen, 1980). 공극률 또는 밀도와 같은 물리적 변수들이 낮은 변동계수를 가질 때, 토양 특성 변화에 따른 용질 이동 및 지하수 오염 평가는 상당한 불확실성을 가지게 된다(Bresler and Dagan, 1981).
연구지역은 경주시 중 ‧ 저준위 방사성폐기물 처분장 부지로, 지역 내 표층처분시설 건설을 추진 중이다. 이 표층처분시설 부지 하부에는 균열 암반(혼펠스)의 불포화대가 존재하고 있다. 본 연구는 균열 암반(혼펠스)으로 구성된 불포화대에서의 수리적인 특성을 파악하기 위해 수리전도도와 불포화함수 매개변수와의 상관성을 분석하고자 한다. 이 연구는 표층처분시설의 폐쇄 이후 수천년 동안에 방사성핵종이 처분부지 하부의 균열암반내 불포화대를 지나 포화대까지 도달 여부를 평가하는 것과 관련된다.
연구지역의 개관
경주시 중 ‧ 저준위 방사성폐기물 처분장에는 2015년부터 중준위 이하 폐기물을 해수면 아래 지하 80~130 m에 천층처분 방식의 동굴처분시설을 건설하여 운영하고 있다. NSSC(2020)에 의하면, 방사능 농도에 따라 고준위 방사성폐기물은 심층처분만 가능하고, 중준위 및 저준위, 극저준위 방사성폐기물은 천층처분 및 심층처분이 가능하다.
현재 경주중 ‧ 저준위방사성폐기물 처분장에서는 저준위 및 극저준위방사성폐기물을 처분하고자 천층처분방식의 표층 및 매립형처분시설의 개발을 추진하고 있다. 표층 및 매립형 처분시설 운영종료 후, 수백년의 폐쇄 후 관리기간을 지나 수천년이 경과 하면 처분시설의 공학적방벽이 기능을 상실하여 처분고로부터 방사성핵종이 누출되고, 처분시설 하부의 불포화대를 통과하여 포화대까지 도달하여 이동할 수가 있다(Andre-Jehan and Molinas, 1993).
연구지역의 지질은 주로 백악기 퇴적암류(녹회색 또는 담회색의 사암과 녹회색 또는 암회색 셰일)와 화강섬록암, 흑운모 화강암, 섬록암의 제3기 화강암류, 제3기 유문암, 석영안산암으로 구성되어 있다(Chwae et al., 1988; Hwang et al., 2007). 퇴적암은 화강암과의 접촉부에서 열변성작용에 의해서 혼펠스화 되어있다. 연구지역내 지하수의 유동은 주로 화강암과 퇴적암의 소규모 단열대 혹은 단열의 간극을 따라 일어난다(Cheong et al., 2017). 광역적인 지하수 흐름은 서쪽의 산지로부터 동쪽의 해안지역으로 향하고, 국부적으로는 경주 방폐장 운영에 의한 양수로 사일로 및 터널 주변 지하수위가 하강하여 주변 지하수 흐름이 사일로 방향으로 향하고 있다(Cheong et al., 2017).
연구 방법
현장투수시험
수위강하시험
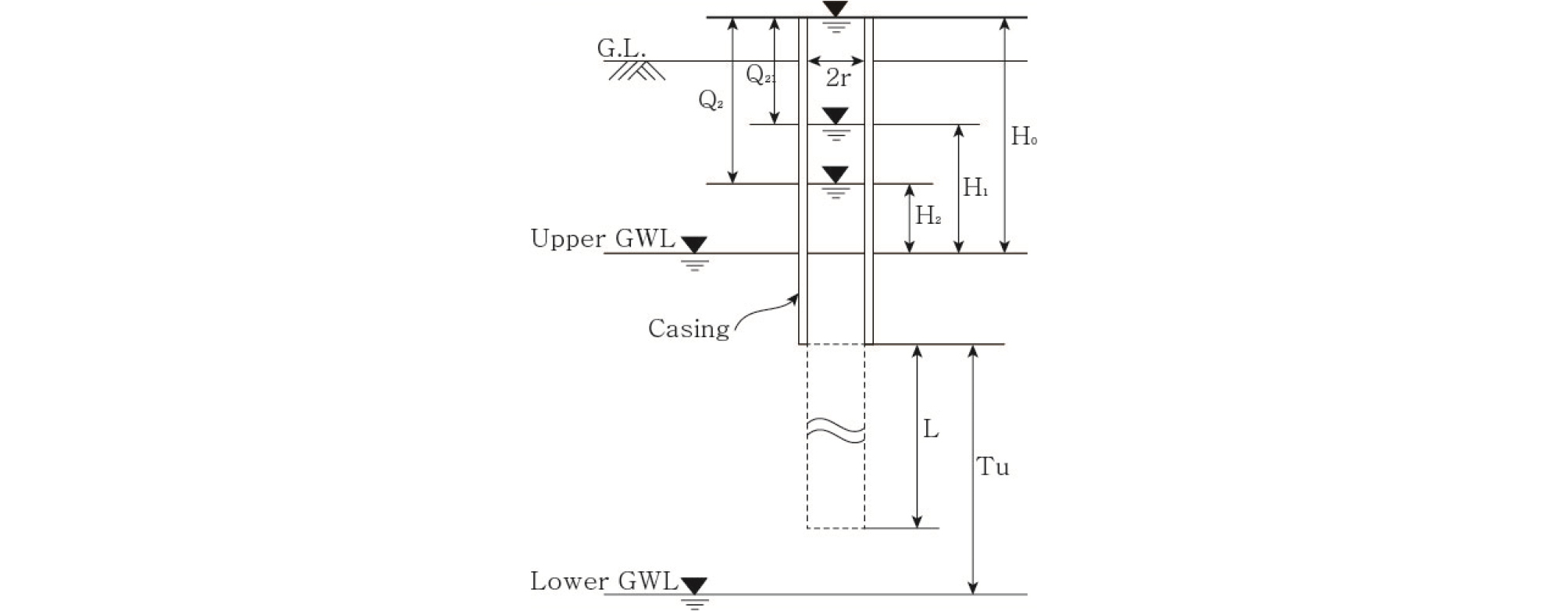
수위강하시험(Falling head test)은 단일패커(Single packer)로 시험구간을 격리하고 청수를 주입한 후 시간 경과에 따른 수위의 변화를 초단위로 측정하는 방법으로서, 패커 하부의 자동수위 센서(다이버)에서 1~2초 간격으로 수위강하를 측정한다. 수위강하시험으로부터는 세 가지 경우에 대한 수리전도도를 도출한다(Horner, 1951). 첫 번째는 이고, 지하수면이 시험구간보다 아래에 있는 경우(Fig. 1의 Lower GWL)로서, 수리전도도는
| $$K=\frac Q{2\pi L^2}\left[2.3\log_{10}\left\{\frac Lr+\sqrt{1+\left(\frac Lr\right)^2}\right\}-1\right]$$ | (1) |
이다. 두 번째는 이며, 지하수면이 시험구간보다 아래에 있는 경우(Fig. 1의 Lower GWL.)로서, 수리전도도는
| $$K=\frac{6.9Q\log_{10}\left(\frac Lr\right)}{2\pi L(L+2Tu)}$$ | (2) |
이다. 세 번째는 이며, 지하수면이 시험구간보다 위에 있는 경우(Fig. 1의 Upper GWL)로서,
| $$K=\frac{r^2}{2L(t_2-t_1)}\ln\left(\frac Lr\right)\ln\left(\frac{H_1}{H_2}\right)$$ | (3) |
이다. 여기서, K는 수리전도도이고, r은 케이싱의 반지름, L은 시험구간의 길이(L > 0), Tu는 공저에서 지하수면까지의 거리, H0은 초기수두, H1은 시간 t1일 때의 수두, H2는 시간 t2일 때의 수두, Q1은 시간 t1일 때 우물로의 유입량, Q2는 시간 t2일 때 우물로의 유입량이다.
정압주입시험
정압주입시험(Constant injection pressure test)은 시험구간에 일정한 압력으로 시험수를 주입할 때 주입량과 주입에 의한 압력을 측정하여 암반의 수리전도도를 구하는 시험으로 주입단계와 수두강하단계의 두 단계로 구성된다(Vaskou et al., 2019).
주입단계 시험(Injection phase test)을 위해서는 먼저 시험구간에 패커를 설치하고, 유량계와 압력계를 설치한다. 그리고 일정 압력을 유지시킨 상태에서 15~20분 동안 시험구간에 물을 주입한다. 주입 압력은 통상 수두(즉, 시험구간의 지하수위)보다 약 0.5~1.0 bar 더 크게 한다. 이 때, 현장의 지질 조건에 따라 압력을 조정하여 암반 파쇄가 일어나지 않도록 조심하여야 한다. 물을 주입하는 동안 주입압력과 물의 주입량을 기록하고, 일정 압력이 유지되는 상태까지 물을 주입 후 주입단계 시험을 종료한다. 수두강하단계 시험(Fall-off phase test)은 주입 종료와 동시에 주입 밸브를 닫아 외부와 완전히 차단하고, 주입단계보다 오랜 시간(3~4배 기간) 동안 주입압력 해소에 따른 수두강하를 기록하는 것이다.
정압주입시험의 주입단계는 정상류 상태로 가정하며, Moye(1967) 식과 U.S. Bureau of Reclamation(USBR, 1977) 식으로 수리전도도를 산출한다. Moye(1967) 식에 의한 수리전도도(K)는
| $$K=\frac q{LH_0}\left[\frac1{2\pi}\left(1+\ln\left(\frac L{2r_w}\right)\right)\right]$$ | (4) |
이다. 여기서, q는 주입율(m3/s), L은 시험구간 길이(m), H0은 유효 주입수두(m), rw는 시추공 반경(m)이다.
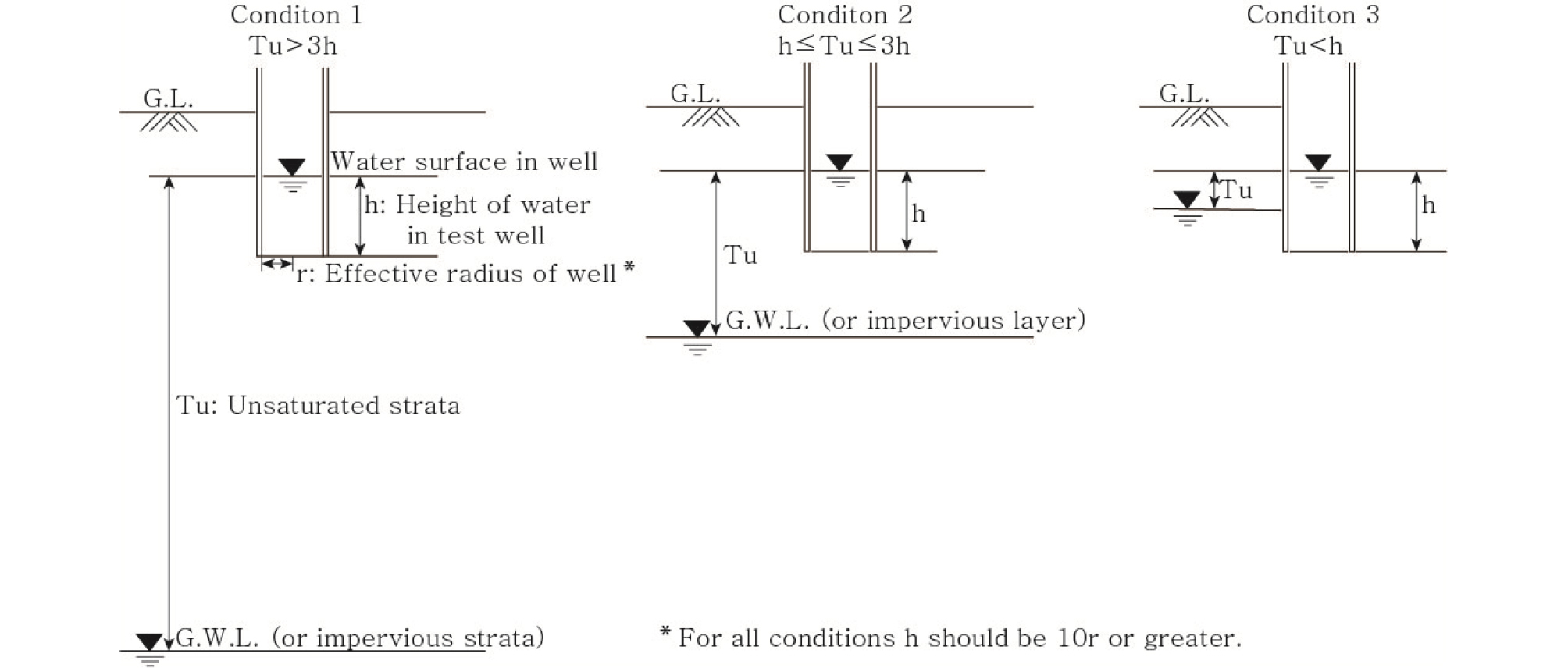
USBR(1977) 법은 나공(Open hole)에 적용하며 세 가지 지하수위 조건에 대한 수리전도도를 구한다(Fig. 2). 시험구간보다 깊은 심도에 지하수위가 위치하는 조건(조건 1)에서 수리전도도는
| $$K=\frac{2Q}{(C_s+4)rTu}$$ | (5) |
이다. 시험구간 직하부에 지하수위가 위치하는 조건(조건 2)에서 수리전도도는
| $$K=\frac{2Q}{\left[C_s+4\left(\frac r{r_e}\right)\right]r_e(Tu+h-A)}$$ | (6) |
이다. 그리고 시험구간 내에 지하수위가 존재하는 경우(조건 3)의 수리전도도는
| $$K=\frac{2Q}{\left[C_s+4\left(\frac r{r_e}\right)\right]r_eTu}$$ | (7) |
이다. 여기서
| $$C_s=\frac{2\pi(A/r)}{\ln(A/r)}$$ | (8) |
이다. 그리고 r은 케이싱의 반지름(m), re는 시추공 유효 반경(m, 스크린을 사용하지 않는 경우, re = r), Tu는 공저에서 지하수면까지의 거리(m), h는 시추공에서의 물의 높이(m), A는 시험구간의 길이(m)이다.
한편 수두강하단계에서는 부정류 해석법인 Horner(1951) 식을 적용하여 수리전도도(K)를 산출한다:
| $$K=\frac{0.183Q_p}{\triangle(dp')L}$$ | (9) |
여기서, Qp는 주입율, ∆(dp')는 압력 변화/1 log cycle(m), L은 시험구간(m)이다.
불포화 실내실험분석
불포화함수 모델
다공질 매질 내에는 일반적으로 두 종류 이상의 유체가 공존한다. 상호 평형을 이루는 과정에서 유체들 간에는 경계면(interface)이 형성되고 모세관현상이 나타난다. 유체와 유체간의 경계면은 고체막(solid membrane)과 같은 역할을 하며 표면장력(σ)에 따라 증대된다. 이때 표면장력은 두 유체의 압력차 즉, 모세관압(Capillary pressure)을 발생시킨다. 모세관압(Pc)은 두 유체간의 경계면이 이루는 곡면의 함수로서 아래 식과 같다(Fredlund et al., 2012):
| $$P_c=\sigma\left(\frac1{R_1}+\frac1{R_2}\right)$$ | (10) |
위 식에서 R1과 R2는 두 유체간 경계면을 중심으로 각각 두개의 곡면의 주 반지름을 의미한다. 표면장력은 단위길이당 힘으로 표현되며 N/m 혹은 mN/m(= dyne/cm) 단위를 가진다. 수은/수은증기의 표면장력은 485 mN/m로서 물/공기의 표면장력인 72.75 mN/m보다 6.7배 정도 더 크다(Mine et al., 2015).
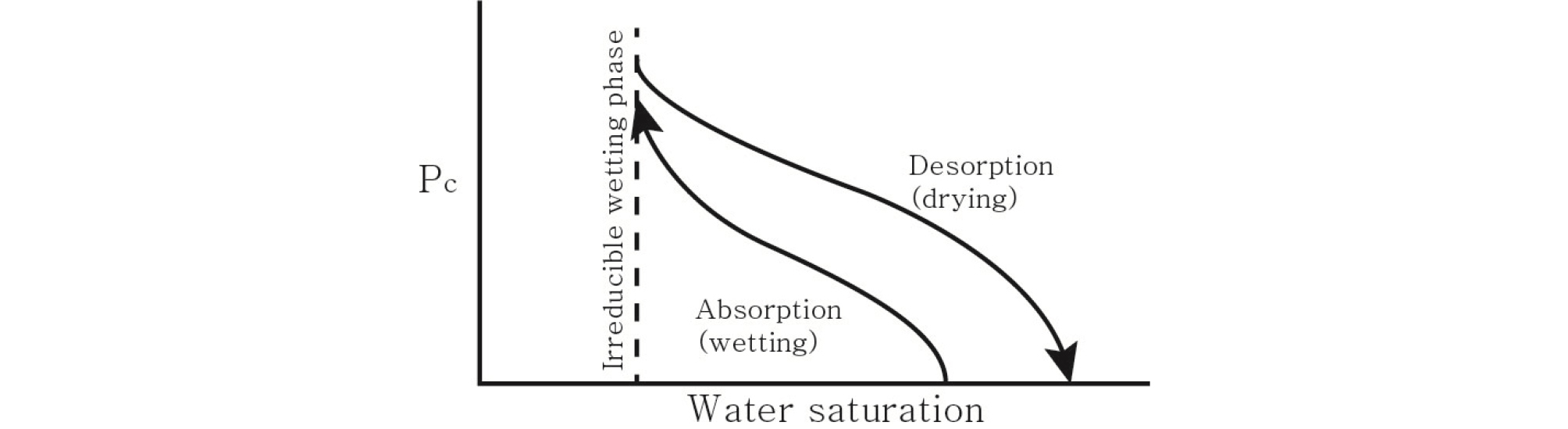
유체가 다공질 매질의 더 작은 공극 속으로 침투하기 위해서는 소수성(non-wetting) 유체가 계속해서 높은 모세관 압력 하에 있어야 한다. 따라서 모세관 압력과 유체의 포화도는 음의 상관관계를 갖는다. Fig. 3은 물의 포화도에 따른 모세관 압력 관계를 나타내며, 다공질 매질에서 2상 유체(two-phase fluid)의 특성을 반영한다(Dake, 1998).
모세관압력(Pc)은 Brooks and Corey(1964) 모델, van Genuchten(1980) 모델 등으로 표현된다.
| $$P_c=P_0(\lbrack S^\ast\rbrack^{-1/\lambda}-1)^{1-\lambda}$$ | (11) |
| $$S^\ast=\frac{S_w-S_{wir}}{1-S_{wir}}=\left(\frac1{1+(\alpha\Psi)^n}\right)^m$$ | (12) |
여기서, P0는 강도계수(strength coefficient), λ는 공극의 분포특성 인자, Sw는 물의 포화도, Swir은 물의 잔류포화도, ψ는 모세관압력이다. ψ가 가스진입압력(ψa)와 같거나 크면 S*는 1이다.
Van Genuchten(1980)에 의한 불포화수리전도도는
| $$K_{un}=K_{s} {S^{\ast}}^{\frac12}\left\{1-\left[1-S^{\ast^\frac1m}\right]^m\right\}^2$$ | (13) |
여기서, Ks는 포화수리전도도이고,α와 n은 반 게누텐 매개변수이고, m은 물포화도-모세관압 곡선의 매개변수로써, 1-1/n과 같다.
수은주입 모세관압 실험
수은주입 모세관압(Mercury Injection Capillary Pressure, MICP) 실험은 공극률, 공극크기 분포도, 포화도에 따른 모세관압을 구하는 것이다. 소수성 유체인 수은은 외부로부터 압력이 가해져야 미세 공극에 침투할 수 있으며, 공극의 크기가 작을수록 높은 압력이 요구된다. 이때의 압력과 침투한 수은의 포화도를 물/공기 시스템의 값으로 변환하여 물포화도에 따른 모세관압 곡선을 산정하고, 그 결과로부터 반 게누텐 매개변수를 도출한다.
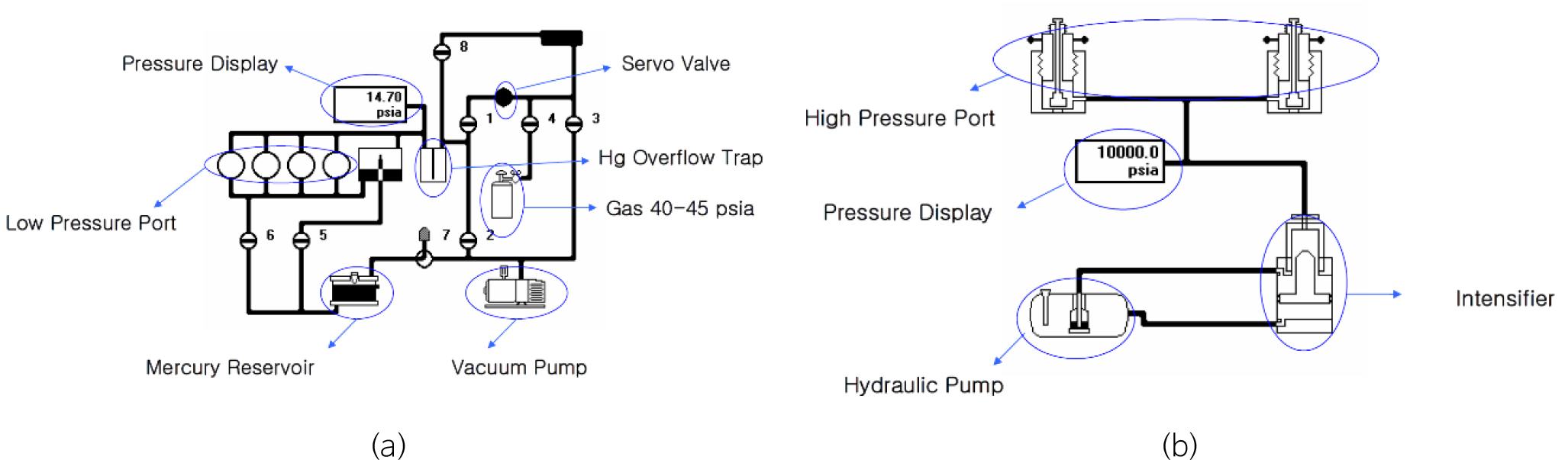
수은주입 모세관압 실험에서는 수은주입 공극률 측정기(mercury injection porosimeter, 미국 Micromeritics사의 모델 AutoPore IV)를 사용하여 암석시료를 대상으로 수은의 압력을 점차 증가시키면서 암석내로 주입되는 수은의 양을 측정한다. 실험을 위해서는 먼저 열린 공극(단열)이 있는 암석시료를 약 1 cm3 크기로 만들어서 세척한다. 암석시료를 60℃에서 24시간 이상 건조시킨 후 무게를 측정한다. 그리고 시료를 침입도계(penetrometer)에 넣고 밀봉한 후 진공 상태에서 수은을 채워 넣는다. 먼저 저압포트(low-pressure port)에서 50 µm Hg 압력(진공상태)하에 시료에 수은을 채운 후, 저압(30 psi)으로 시료에 수은을 주입한 후 무게를 재측정하여 총밀도를 산정한다. 그 다음에는 고압포트(high-pressure port)에서 압력을 최대 60,000 psi까지 증가시키면서 시료에 수은을 주입하게 된다(Fig. 4).
침입도계에 압력이 가해지면 수은이 공극내로 침투하여 스템(stem) 내에 수은의 부피가 감소하는데 이 감소를 압력의 함수로 산정하면 공극에 침투한 수은의 부피를 알 수 있다. 즉, 공극의 크기 또는 침투 압력에 따른 시료 질량당 침투된 수은의 누적부피(cumulative penetration volume)를 알 수 있게 된다.
결 과
현장수리시험 분석결과
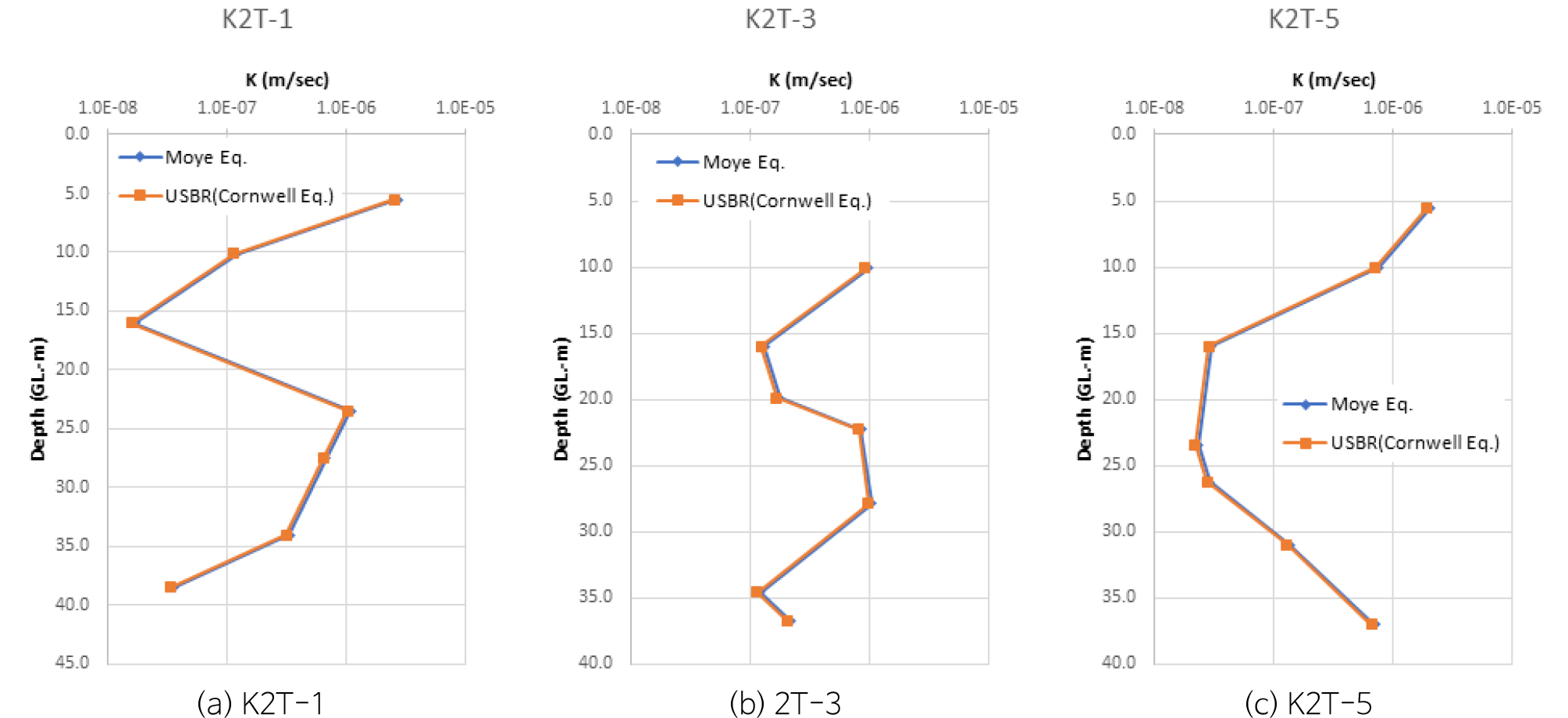
표층처분시설의 수리지질학적 특성을 파악하기 위해 부지 내 및 인근에서 K2-1~3, 2KB-1~4, GM2-1-1~GM2-1-3, GM2-2-1~GM2-2-3, GM2-3-1~GM2-3-3, GM2-4-1~GM2-4-3, GM2-5-1~GM2-5-3, K2T-1~19, PW8-1~PW8-3, PW9-1~PW9-3, PW10-1~PW10-3의 총 50개공을 굴착하였다. 이들 시추공에서 지층(토양층, 풍화대, 암반)의 불포화대 구간에 대하여 총 481회의 수리시험(수위강하시험 231회, 정압주입시험 250회)을 수행하여 수리전도도를 구하였다. 현장에서 수위강하시험은 기본적으로는 6 m 간격으로 실시하였으나, 파쇄대, 단열대 등의 암반상태에 따라 시험구간을 변경하기도 하였다. 현장수리시험 결과를 Moye 식과 USBR 방법에 적용하여 수리전도도를 구한 결과, 9.95 × 10-5 ~ 3.06 × 10-11 m/sec의 범위를 보이고, 기하평균은 1.51 × 10-7 m/sec이다(Table 1). 심도에 따른 수리전도도는 K2T-1, K2T-3, K2T-5에서 모두 15 m 심도까지는 감소한다(Fig. 5). 그리고 K2T-1과 K2T-3 공에서는 약 25~30 m 심도까지 수리전도도가 증가하다가 그 보다 깊은 심도에서는 다시 하강하는 경향성을 보인다. 그러나 K2T-5 공에서는 약 15~25 m에서 낮은 값을 보이다가 그 보다 깊은 심도에서는 증가하는 경향성을 보인다.
Table 1.
Result of in-situ hydraulic tests
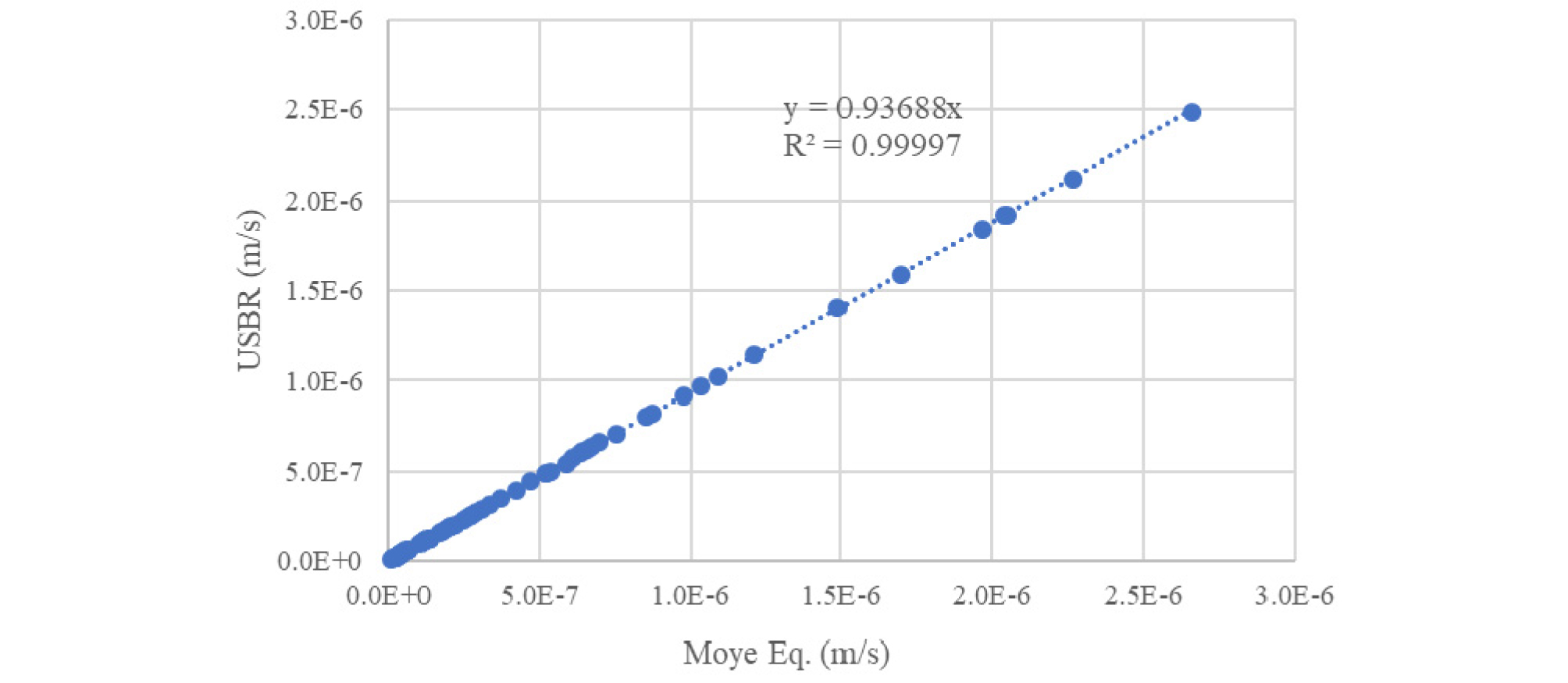
정압주입시험 중 K2T-1~10 시추공에 대해서는 Moye 식과 USBR 방법으로 구한 수리전도도를 서로 비교하였다(Fig. 6). 불포화대 구간의 정압주입시험을 수행한 K2T 시추공들은 시추공 바닥(해발 67 m)보다 지하수위가 27 m 더 낮은 해발 40 m에 위치하므로 지하수위가 시험구간(h = 6 m)의 3배 보다 더 아래에 위치하여 USBR 방법의 조건 1을 적용하였다.
K2T-1~10 시추공의 정압주입시험 결과에 대해서 Moye 식과 USBR 방법에 의한 수리전도도를 서로 비교했을 때, Fig. 6과 같이 두 식의 수리전도도가 서로 매우 높은 상관성(상관계수 0.9999)을 보인다.
실내실험 분석 결과
실내실험을 통해 3개의 시추공(2KB-1, 2KB-2, 2KB-3) 10개 구간 시추 시료에 대한 공극률, 공극크기 분포도 그리고 포화도에 따른 모세관압을 측정하고, 수은 주입 모세관압(MICP) 분석을 수행하여 측정된 포화도에 따른 모세관압 곡선을 도출하였다. 그리고 반 게누텐 모델에 적용하여 매개변수 P0, λ, α, n을 도출하였다.
실험결과, 시료의 총밀도는 2.479~2.727 g/ml, 공극률은 0.04~0.32%이었다. 또한 MICP를 이용하여 코어시료에 소수성인 수은을 주입하면서 건조주기의 함수율에 따른 모세관압을 측정하였다. 반 게누텐 모델로 구한 P0는 8,000~15,000 Pa, λ는 0.5~0.75, α(기체진입압력 관련 매개변수)는 0.200~0.375, n(형상관련 매개변수)은 2.0~4.0로 산정되었다(Table 2). Yang and You(2013)에 의하면, 사질양토의 경우 n값은 1.1~1.4 정도이며 본 연구지역과 같은 균열 암반에서는 이보다 높은 2.0~4.0의 범위를 보인다. 이는 단열 간극의 거칠기가 토양층의 입자들 보다 크기 때문으로 판단된다. 한편, 사질양토의 경우에는 α값이 대체로 0.5~0.6인 반면 본 연구지역에서는 0.2~0.4의 분포로 더 작게 나타난다. 이는 α값이 수리전도도와 비례하며, 사질양토의 수리전도도보다 본 연구지역의 균열 암반의 수리전도도가 더 낮기 때문이다.
Table 2.
Hydraulic property and van Genuchten parameters of unsaturated hornfels
현장 수리전도도와 실내 불포화 매개변수의 상관성 분석
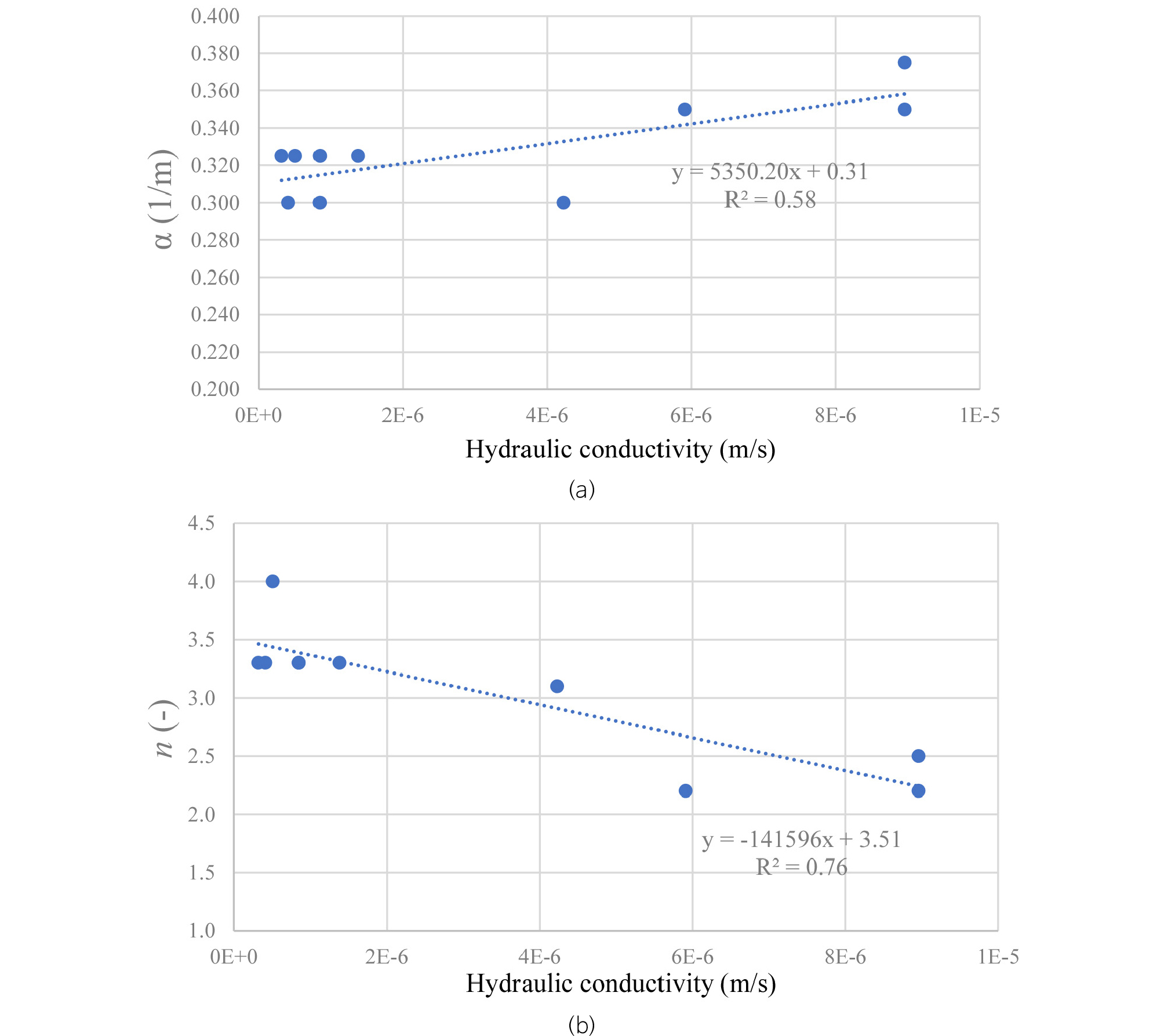
현장수리시험을 실시한 50개의 시험공 중 실내실험을 수행한 3개 시험공(2KB-1,2KB-2, 2KB-3) 10개의 심도 구간으로부터 산출된 포화수리전도도와 실내실험에서 도출된 반 게누텐 매개변수(α, n)의 상관성을 분석하였다(Fig. 7).
표층처분시설 부지내 2KB-1~3공의 포화수리전도도 값과 반 게누텐 매개변수 α의 상관계수는 0.7607이고, 상관식은
| $$\alpha=5350.20\times K+0.31$$ | (14) |
이다. 한편, 현장 수리전도도 값과 반 게누텐 매개변수 n의 상관계수는 -0.8720이고, 상관식은
| $$n=-141596\times K+3.51$$ | (15) |
이다. 결과적으로 포화수리전도도와 α간에는 양의 상관성이 나타나고, 포화 수리전도도와 n간에는 음의 상관성이 나타난다. 이는 기체진입압력(Gas entry pressure) 관련 매개변수인 α가 포화수리전도도에 비례한다는 것을 나타낸다. 일반적인 경향성과 마찬가지로 연구지역의 불포화 혼펠스 암반 단열에서도 포화수리전도도가 커질수록 모세관압이 작아지는 경향성이 잘 나타나고 있다. 또한, 포화수리전도도는 형상관련 매개변수 n과 반비례하는데, 이는 연구지역내에서는 포화수리전도도가 단열 간극의 거칠기와 반비례한다는 것을 의미한다. 이러한 상관관계를 기반으로 암반의 불포화대 구간에서 실시된 현장 포화수리전도도 값을 알면, 반 게누텐 매개변수 α와 n을 도출할 수 있다. 도출된 반 게누텐 매개변수는 불포화대 지하수 유동 모델링의 입력인자로 활용될 수 있다.
토 의
현장수리시험에서 구한 포화수리전도도와 실내실험으로 도출된 반 게누텐 매개변수(α, n)의 상관성을 분석한 결과, 포화수리전도도와 α간에는 양의 상관성이 나타나는 반면에, 포화수리전도도와 n간에는 음의 상관성이 나타난다. 이는 연구지역내에서는 포화수리전도도가 단열 간극의 거칠기와 반비례한다는 것을 의미한다. 도출된 포화수리전도도 값과 반 게누텐 매개변수 α, 포화수리전도도와 n의 상관식을 이용하면, 혼펠스 암반의 불포화대 구간에서 포화수리전도도 값만으로도 반 게누텐 매개변수인 α와 n 값 그리고 불포화수리전도도를 추정할 수 있다.
본 연구지역과 같은 불균질한 균열 암반 지역에서는 규모종속 효과에 의해서 수리전도도가 달라진다. 즉, 암반의 불균질성에 의해서 발생하는 규모종속 효과에 의해서 암반의 부피가 증가할수록 수리전도도는 증가하는 경향성이 있다(Martinez-Landa and Carrera, 2005). Martinez-Landa and Carrera(2005)는 등가 수리전도도(equivalent hydraulic conductivity)와 점 수리전도도(point hydraulic conductivity)의 관계에 의해서 규모종속 효과를 해석할 수 있다고 보고하였다. 본 연구에서는 실내실험 규모(금번 연구에서는 부피 약 1 cm3)와 현장시험 규모 간의 규모종속 효과에 의한 수리전도도 변화를 상세하게 분석하지는 않았으나, 실내실험과 현장수리시험을 비교하여 규모의 변화에 따른 수리전도도 값들 간에 상관성이 있다는 것을 확인하였다.
결 론
경주 방폐장 표층처분시설 혼펠스 지역의 불포화대 수리지질학적 특성을 파악하기 위한 방법으로써 현장수리시험으로 포화수리전도도를 산출하고 수은주입 모세관압 실험 결과와 반 게누텐 모델로 매개변수 α와 n을 도출하여, 포화수리전도도와 매개변수 α와 n간의 상관성을 분석하였다.
50개 시추공의 481개 지점 현장수리시험 결과, 수리전도도는 9.95 × 10-5 ~ 3.06 × 10-11 m/sec의 범위를 보이고, 기하평균은 1.51 × 10-7 m/sec의 값을 나타낸다. 3개 시추공 10개 지점의 시료에 대한 실내실험분석 결과, 기체진입압력 관련 매개변수 α는 0.200~0.375 1/m의 범위를 보이고, 형상관련 매개변수 n은 2.0~4.0의 범위를 보인다.
현장수리시험과 실내실험분석이 동시에 이루어진 3개 시험공의 10개 심도 구간에 대한 수리전도도와 불포화 매개변수 α, n에 대한 상관성분석에 의하면, 수리전도도와 매개변수 α의 상관계수는 0.7607이고, 수리전도도와 불포화 매개변수 n의 상관계수가 -0.8720이다. 이는 연구지역의 불포화 암반(혼펠스)에서의 현장수리전도도와 실내실험에 의한 불포화 매개변수 간에는 상당히 높은 상관성이 존재한다는 것을 지시한다.
향후에는 수리전도도의 규모종속 효과를 보다 상세히 분석하여, 수리전도도를 부지에 적용 시에는 큰 규모와 단일 단열 규모의 차이를 명확하게 구분할 필요가 있을 것이다. 금번 연구 결과가 규모종속 효과의 불확실성을 내포하고 있으나, 실내실험값과 현장수리시험값의 상관식을 바탕으로 현장수리시험에서 구해진 수리전도도값을 대입하여 불포화 매개변수값이 구해지지 않은 특정 지점의 불포화 매개변수값을 도출하고 이를 불포화대 유동모델링의 입력인자로 활용할 수 있을 것으로 판단된다. 또한 연구지역의 불포화대 모델링에 의해서 불포화대 구간의 공간적인 해석이 가능할 것이다. 아울러서 이러한 연구는 국내 표층처분방식 방사성폐기물 처분부지 개발에 적용함으로써 처분시설 폐쇄 이후 장기간에 걸쳐 방사성핵종이 천층처분부지 하부의 불포화대를 지나 포화대까지 도달하는 과정을 규명하는데 도움을 줄 수 있다.