서 론
지진이나 발파와 같이 외부에서 발생된 진동이 지각 구성물질이나 구조물에 미치는 영향을 평가하기 위해서는 지반의 동적 특성을 파악하는 것이 중요하다. 암반의 동탄성계수는 지각 구성물질의 동적 특성을 파악하기 위한 중요한 역학적 특성중 하나이다. 암석 또는 암반의 동적 특성은 반복하중이나 비틂하중 등을 이용한 시험을 통해 측정될 수 있으나 시험이 복잡하고 시간이 많이 소요된다. 따라서 초음파나 탄성파를 이용한 시험을 통해 동적특성 추정과 정적특성과 동적특성을 비교하는 연구가 많이 진행되고 있다.
동적특성의 결정은 초음파 또는 탄성파 시험을 수행하여 P파와 S파의 속도를 측정한 후 경험식에 의해 간접적으로 산정할 수 있다(Stan and Idziak, 2008; Min et al., 2011; Kumar et al., 2015). 초음파를 이용한 측정방법은 비파괴 검사방법이면서, 다른 방법들에 비해 상대적으로 간편하고 빠르게 진행할 수 있기 때문에 많이 이용된다. Stan and Idziak(2008)은 암반에 존재하는 균열의 방향성을 고려하여 P파와 S파의 속도를 측정하고, 동적특성을 추정하여 균열에 따른 암석의 이방성에 대한 연구를 수행하였다. Altindag(2011)는 P파 속도와 단위중량, 공극률, 쇼어경도, brittleness, 일축압축강도, 인장강도, 점하중강도, 탄성계수 등 다양한 역학적 특성의 관계식을 제시한 바 있다. Sukplum et al.(2014)는 사암의 층리면에 수직 및 수평방향으로 채취한 시료를 대상으로 층리면 방향에 따른 S파 및 P파 속도, 정탄성계수, 동탄성계수를 비교하여 각 인자들의 상관성을 제시하였다. Chawre(2018)은 S파 및 P파 속도와 공극률, 밀도, 일축압축강도 등 암석의 물리적인 특성의 상관성을 분석한 바 있다. 이외에도 정적특성과 동적특성의 비교 분석을 통해 동적 특성을 추정하고자 하는 연구가 많이 진행되어 왔다(King, 1983; Christaras et al., 1994; Ameen et al., 2009; Martínez-Martínez et al., 2012; Sone and Zoback, 2013; Chawre, 2018). 이와 같이 여러 연구자들에 의해 암석의 정적특성과 동적특성의 상관성이 입증되면서 초음파를 이용한 암석의 정적 그리고 동적특성의 평가는 유용한 것으로 평가되고 있다.
본 연구에서는 국내 40개 구조물 설계 시 수행된 1,646개의 실내 및 현장시험 결과를 대상으로 암종별 P파 속도, 동탄성계수, 정탄성계수의 분포특성을 분석하였다. 또한 비교적 획득이 쉬운 P파 속도를 통해 동탄성계수를 쉽게 추정할 수 있도록 P파 속도와 정탄성계수의 관계, 정탄성계수와 동탄성계수의 관계, P파 속도와 동탄성계수의 관계에 대한 상관식을 제안하고 기존 연구사례와 비교하여 검증하였다.
수집자료 및 분포특성
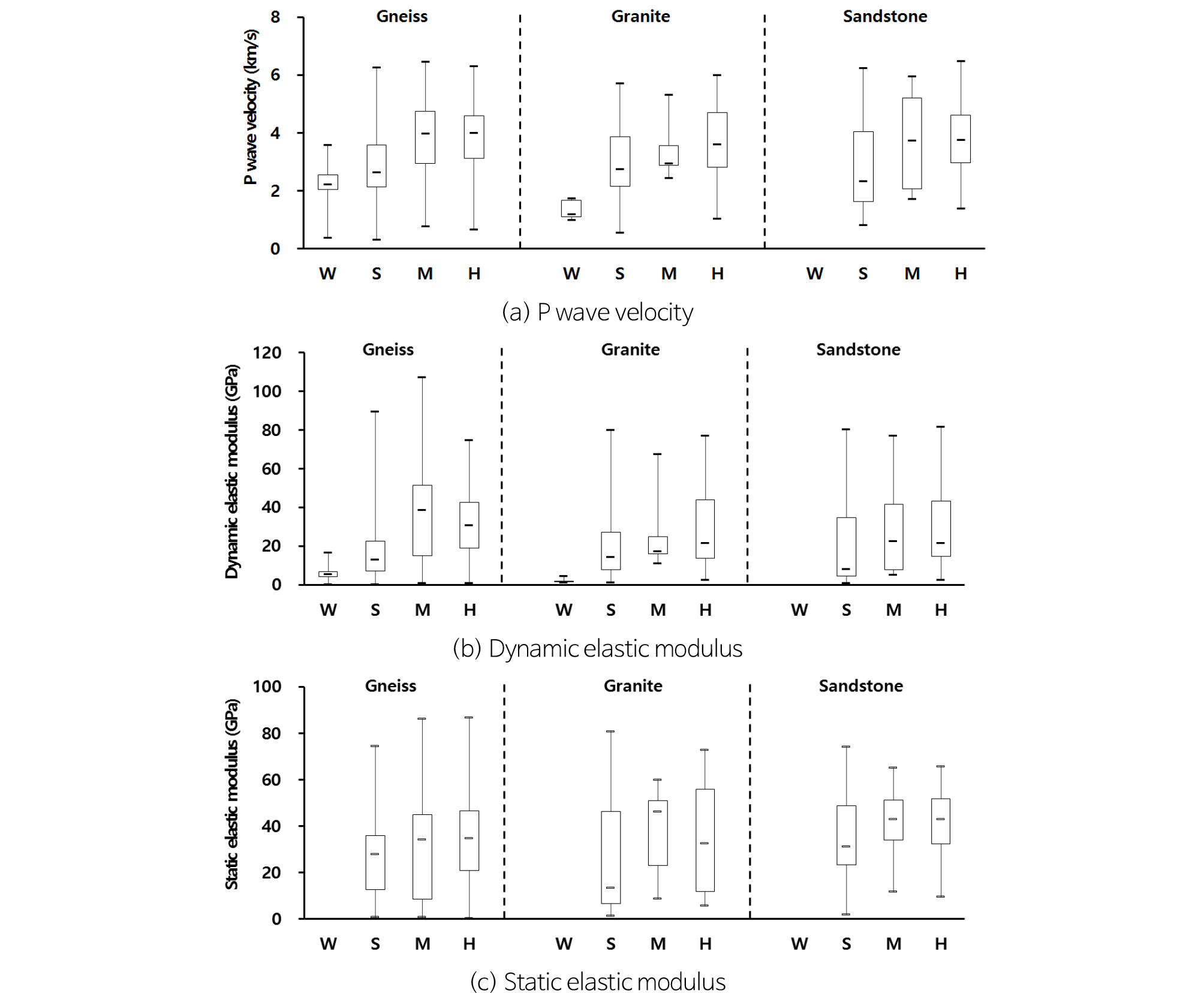
분석에 이용된 데이터는 총 1,646개의 실내 및 현장시험 결과이며, P파 속도, 동탄성계수, 정탄성계수 등을 결정하기 위해 초음파 시험, 탄성파 시험, 업홀 시험과 크로스홀 시험(다운홀 시험, SPS 로깅 포함), 다중채널 표면파 탐사(Multichannel Analysis of Surface Wave, MASW) 등이 적용되었다. 수집된 자료는 암종별로 편마암 862개, 화강암 527개, 사암 257개이다. 동일한 현장에서 시행된 시험으로 획득된 자료라도 암반의 풍화 상태에 따라 역학적인 특성이 달라질 수 있기 때문에 각 암종에 대하여 암석의 강도를 기준으로 P파 속도, 동탄성계수, 정탄성계수 분포현황을 상자그림으로 도시하였다(Fig. 1).
상자(box) 내 검은선은 중앙값(median)에 해당하며, 크기순으로 데이터를 배열했을 때 상위 25%와 75%에 해당하는 제1사분위수와 제3사분위수를 각각 상자의 윗면과 아랫면으로 표현하였다. 그러므로 상자의 범위는 전체 데이터의 50%가 분포하는 영역인 사분위수 범위(interquartile range, IQR)를 의미한다. 상자 밖의 수염(whisker)은 데이터의 최댓값(maximum)과 최소값(minimum)을 나타낸다.
P파 속도는 모든 암종에서 경암(hard rock)일 때 중앙값이 가장 크며, 모든 암석강도에서 사암의 IQR이 가장 넓은 분포범위를 보인다(Fig. 1a). 동탄성계수의 경우 편마암-보통암(moderate rock)에서 IQR의 범위가 1.50~5.15 GPa로 가장 넓고, 가장 큰 중앙값을 보인다(Fig. 1b). 정탄성계수는 편마암과 사암에서 암석의 강도가 증가함에 따라 중앙값도 증가하는 경향을 보이며, 화강암의 경우 경암보다 연암(soft rock)에서 높은 중앙값을 보인다. 화강암-연암의 정탄성계수 평균은 37.57 GPa이고, 화강암-경암은 34.01 GPa로 전체적으로 연암의 정탄성계수가 큰 것을 알 수 있다.
P파 속도와 정탄성계수
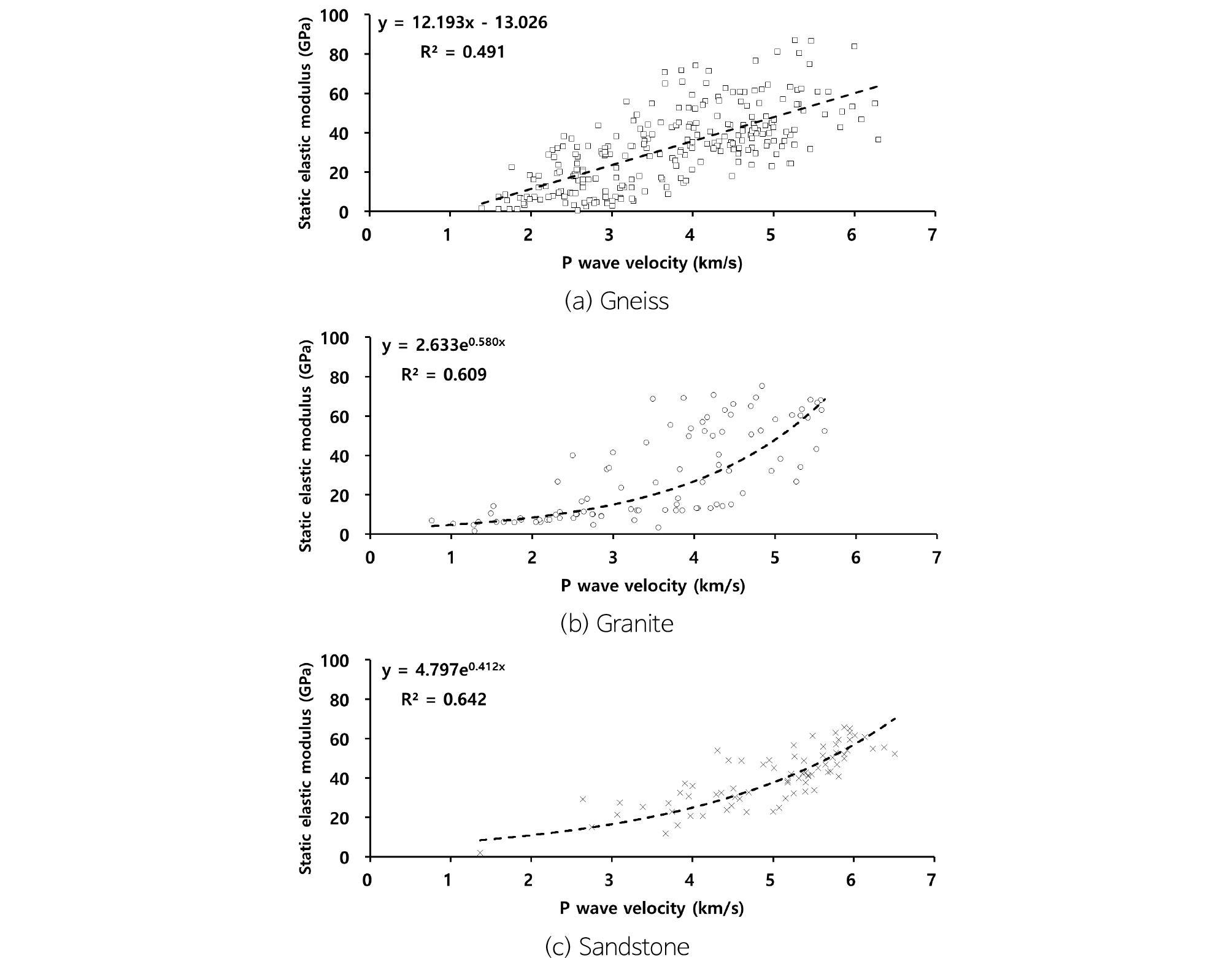
동일한 시료에서 측정된 P파 속도와 일축압축시험으로부터 산정된 정탄성계수의 상관성을 분석하면 Fig. 2와 같다. 편마암은 선형적인 관계를 보이며, 화강암과 사암은 지수함수의 관계를 보인다. 상관관계에 대한 결정계수(coefficient of determination, R2)는 사암에서 0.642로 가장 높게 나타났으며, 편마암에서 0.491으로 가장 낮게 나타났다. P파 속도와 정탄성계수의 상관식에 대한 결정계수가 높은 편에 속하는 것은 아니지만 모든 암종에서 P파 속도가 증가할 때 정탄성계수도 증가하는 경향성을 보이고 있다.
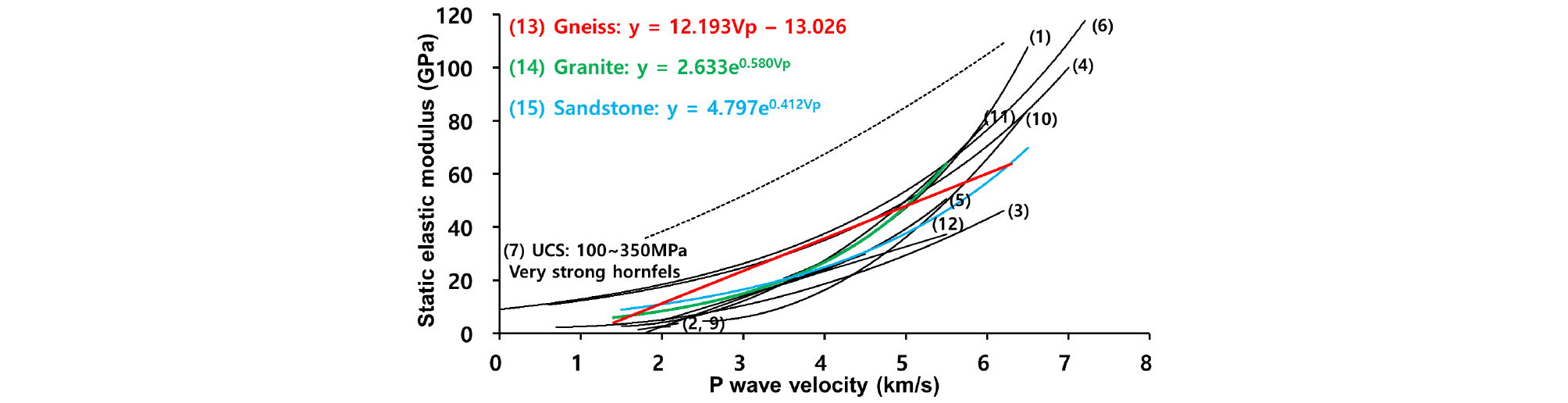
Table 1은 P파 속도와 정탄성계수의 상관관계에 대한 기존 문헌들을 요약한 것이다. 일부 연구자들은 P파 속도와 정탄성계수의 관계를 선형적인 관계로 주장하였으며(Khandelwal and Singh, 2009; Min et al., 2011; Verma et al., 2012; Chawre, 2018), 또 다른 연구자들은 지수함수의 관계를 보인다고 주장한 바 있다(Christaras et al., 1994; Lee et al., 2011; Najibi et al., 2015; Brotons et al., 2016). 그러나 이들이 제안한 P파 속도와 정탄성계수에 대한 상관식을 모두 도시하면 전반적으로 비슷한 경향을 보이는 것을 확인할 수 있다(Fig. 3). 다만, 점선으로 도시된 Lee et al.(2011)의 상관식 (7)은 다른 식들과 비교해서 정탄성계수가 상대적으로 크게 나타나는데, 이는 분석 대상 암종이 UCS 100~350MPa에 해당하는 매우 강한 혼펠스이기 때문에 다소 높게 산정된 것으로 분석된다. 상관식 (7)을 제외하면, 연구자별로 분석 대상 암종이 연약한 탄층부터 단단한 화강암까지 다양하기 때문에 나타나는 편차 범위로 판단할 수 있으며, 이들의 상관식은 결정계수가 0.836~0.990까지 높은 편에 속하므로 신뢰성이 있는 결과로 판단된다. 본 연구에서 확인한 암종별 P파 속도와 정탄성계수의 상관식 (13)~(15)도 기존 문헌에서 제시한 식들의 분포 범위 내에 존재하고, 상관식을 도출하기 위해 이용한 데이터의 수가 비교적 많기 때문에 국내 암종의 분포범위를 파악하는데 활용 가능하다고 판단된다.
Table 1. Relationship between the static elastic modulus (Es) and P wave velocity (Vp) proposed by previous studies and this study. All of the Es values are in GPa
| References | Equation No. | Correlation | R2 | Rock type | Vp range (km/s) |
| Christaras et al.(1994) | (1) | 0.941 | Various | 3.5~6.5 | |
| Khandelwal and Singh(2009) | (2) | 0.974 | Coal layer | 1.7~2.2 | |
| Lee et al.(2011) | (3) | 0.882 | Granite | 0.7~6.2 | |
| (4) | 0.957 | Andesite | 0.6~7.0 | ||
| (5) | 0.836 | Rhyolite | 3.3~5.5 | ||
| (6) | 0.927 | Sedimentary rock | 0.0~7.2 | ||
| (7) | 0.910 | Hornfels | 1.8~6.2 | ||
| Min et al.(2011) | (8) | 0.965 | Granite | 1.8~4.5 | |
| Verma et al.(2012) | (9) | 0.980 | Coal layer | 1.9~2.1 | |
| Najibi et al.(2015) | (10) | 0.900 | Limestone | 2.5~6.5 | |
| Brotons et al.(2016) | (11) | 0.990 | Various | 1.5~6.0 | |
| Chawre(2018) | (12) | 0.890 | Schist | 2.0~5.5 | |
| This study | (13) | 0.466 | Gneiss | 1.4~6.3 | |
| (14) | 0.623 | Granite | 1.4~5.5 | ||
| (15) | 0.662 | Sandstone | 1.4~6.5 |
정탄성계수와 동탄성계수
실내시험으로 측정한 P파 속도와 S파 속도를 이용하여 동탄성계수는 다음 식 (16)~(18)로 구할 수 있다(ASTM D2845-08).
| $$v_d=\frac{{({\displaystyle\frac{V_P}{V_S}})}^2-2}{2{(\frac{V_P}{V_S})}^2-2}$$ | (16) |
| $$G_d=\rho\times V_S^2$$ | (17) |
| $$E_d=\lbrack\rho V_s^2(3V_p^2-4V_s^2\rbrack/(V_p^2-V_s^2)=2G_d(1+v_d)$$ | (18) |
여기서, 는 동포아송비, 는 동탄성계수, 는 동전단탄성계수, 는 단위중량이다.
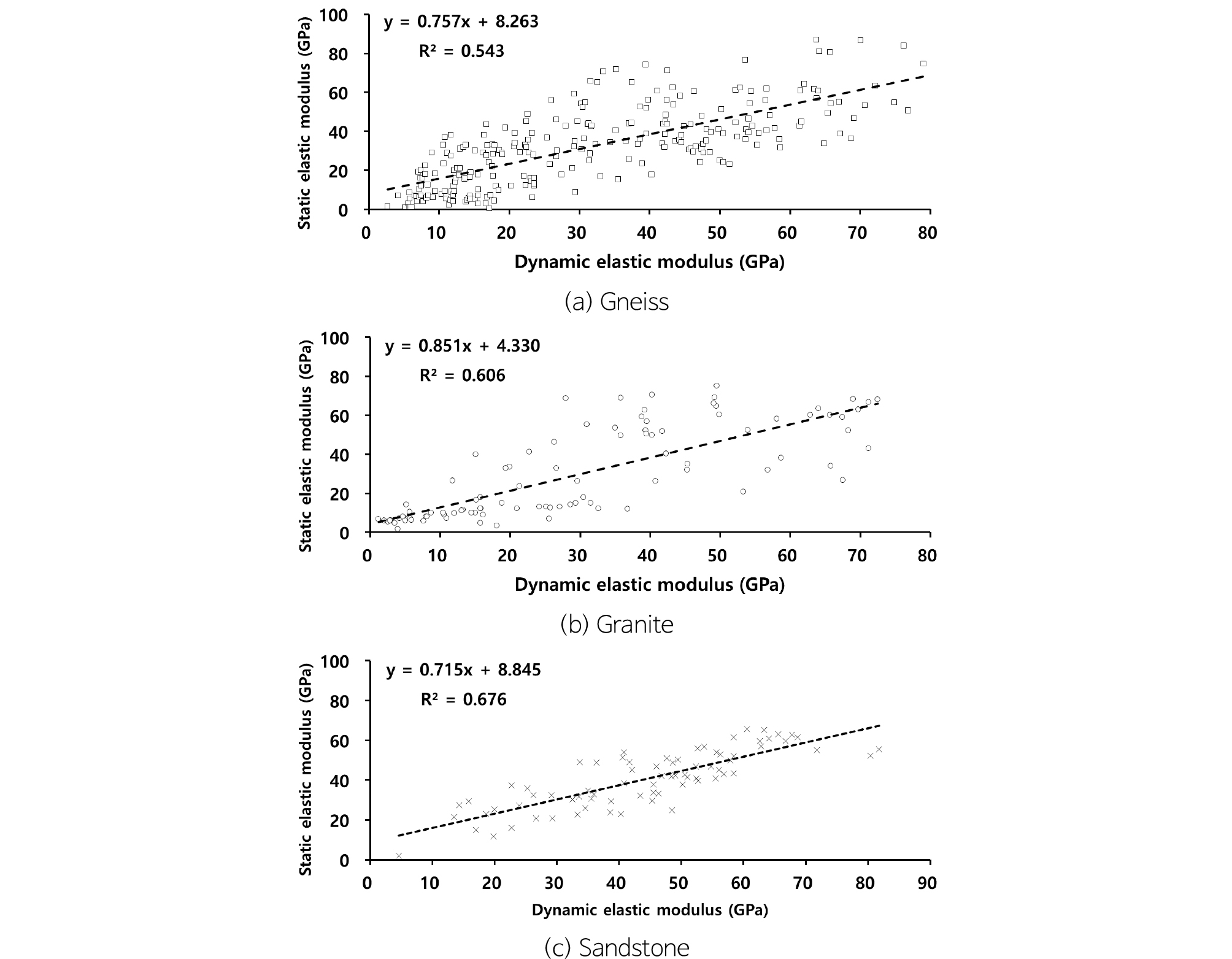
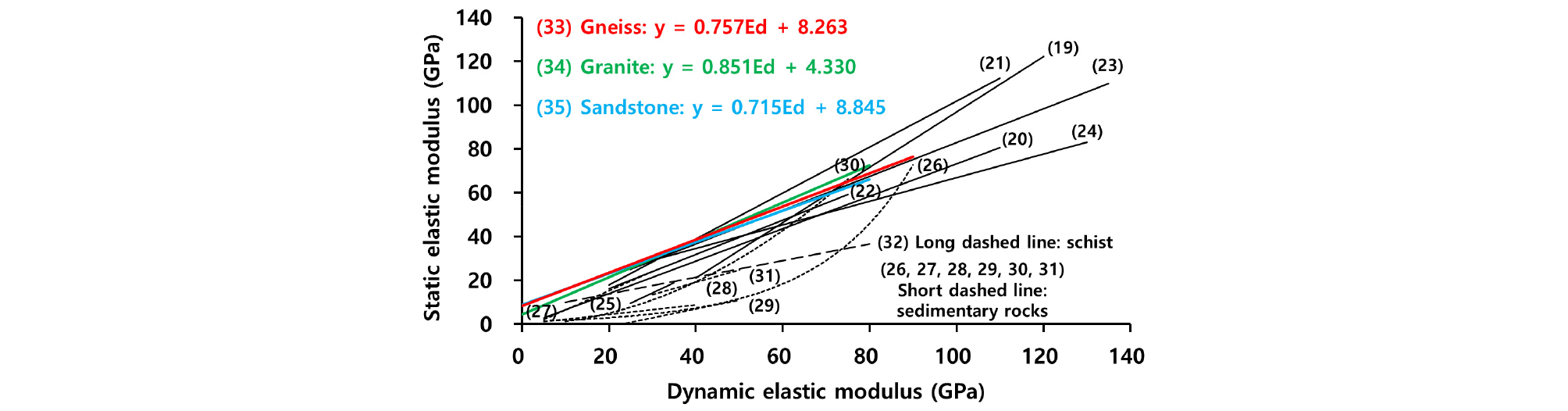
식 (18)로 계산된 동탄성계수와 일축압축강도 시험 결과로부터 결정된 정탄성계수의 관계를 분석하면 Fig. 4와 같다. 두 인자간의 관계는 모든 암종에서 선형의 특성을 보인다. 기울기는 화강암에서 0.851로 가장 높고(Fig. 4b), 사암에서 0.715로 가장 낮게 나타난다(Fig. 4c). 일반적으로 동탄성계수는 정탄성계수보다 큰 경향을 보인다(Simmons and Brace, 1965; King, 1983; Eissa and Kazi, 1988; Ciccotti and Mulargia, 2004). 그 이유는 암석 내 존재하는 균열이나 공극이 증가할수록 동적특성보다 정적특성이 더 크게 감소하기 때문이며, 공극이 많은 암석에서는 정적특정이 동적특성에 비해 작은 값을 보인다(Cheng and Johnston, 1981; King, 1983; Ryu and Chang, 2006; Lee et al., 2008). 본 연구의 결과에서도 동탄성계수가 정탄성계수보다 크게 나타나는 데이터가 편마암(52.0%)이나 화강암(50.0%)보다 사암(61.4%)에서 가장 많이 나타나며, 이는 사암이 일반적으로 공극율이 더 높기 때문인 것으로 판단된다. 또한, 정탄성계수와 동탄성계수의 상관관계에 대한 결정계수(R2)는 사암에서 0.676으로 가장 높게 나타났으며, 편마암에서 0.543으로 가장 낮게 나타났다. 모든 암종에서 결정계수가 높은 편에 속한 것은 아니지만 동탄성계수가 정탄성계수보다 높은 값을 보이며, 두 역학성의 관계는 선형으로 뚜렷한 상관성을 나타내고 있다.
Table 2는 동탄성계수와 정탄성계수의 상관관계에 대한 기존 문헌들을 요약한 것으로서, 많은 연구에서 동탄성계수와 정탄성계수의 선형 또는 비선형 관계를 제안하지만(King, 1983; Eissa and Kazi, 1988; Christaras et al., 1994; Yale and Jamieson, 1994; Mockovčiaková and Pandula, 2003; Min et al., 2011; Brotons et al., 2014; Sukplum et al., 2014; Małgorzata, 2015; Fei et al., 2016; Chawre, 2018), 일부 연구자들은 두 계수의 관계가 비선형이며 여러 매개변수에 의해 결정된다고 주장한다(Soroush et al., 2011; Najibi et al., 2015; Brotons et al., 2016). 기존 연구자들의 결과를 모두 도시하면 Fig. 5와 같으며, 본 연구의 결과는 상관식 (19), (21), (23)과 함께 다른 연구자들의 결과보다 다소 높은 값을 보인다. 이러한 현상은 분석 대상의 암종 차에 기인하는 것으로 판단된다. 상관식 (19), (21), (23)은 화성암-변성암(Igneous-metamorphic rocks)을 포함하는 다수의 암종이 대상이고, 상관식 (33), (34), (35)는 편마암, 화강암, 사암으로 비교적 강도가 높은 암석들이 대상인 반면 점선으로 표시된 연구사례들(상관식 (26)~(31))은 대부분이 상대적으로 강도가 낮은 셰일, 이암, 탄층 등을 포함하는 퇴적암이기 때문에 나타나는 차이인 것으로 판단된다. 본 논문에서 제안한 동탄성계수와 정탄성계수의 상관식은 유사한 암질의 기 연구사례에서 제시한 분포범위에 포함되고 있어 유의한 것으로 판단된다.
Table 2. Relationship between the static elastic modulus (Es) and dynamic elastic modulus (Ed) proposed by previous studies and this study
| References | Equation No. | Correlation | R2 | Rock type | Ed range (GPa) |
| King(1983) | (19) | 0.820 | Igneous-metamorphic rocks | 40~120 | |
| Eissa and Kazi(1988) | (20) | 0.706 | Various | 5~110 | |
| Christaras et al.(1994) | (21) | 0.988 | Various | 20~110 | |
| Yale and Jamieson(1994)* | (22) | 0.902 | Carbonate | 20~75 | |
| Mockovčiaková and Pandula(2003) | (23) | 0.964 | Various | 25~135 | |
| Ameen et al.(2009) | (24) | 0.600 | Sedimentary rock | 20~130 | |
| Min et al.(2011) | (25) | 0.999 | Granite | 25~35 | |
| Soroush et al.(2011)** | (26) | 0.720 | Various (mostly sedimentary rock) | 5~90 | |
| Brotons et al.(2014) | (27) | 0.961 | Calcarenite | 5~30 | |
| Sukplum et al.(2014) | (28) | 0.555 | Clay, Silt, Sand-stone | 5~40 | |
| Małgorzata(2015) | (29) | 0.361 | Shale | 24~50 | |
| Najibi et al.(2015) | (30) | 0.870 | Limestone | 10~75 | |
| Fei et al.(2016) | (31) | 0.725 | Sandstone | 30~50 | |
| Chawre(2018) | (32) | 0.910 | Schist | 10~80 | |
| This study | (33) | 0.543 | Gneiss | 0~90 | |
| (34) | 0.606 | Granite | 0~80 | ||
| (35) | 0.676 | Sandstone | 0~80 |
**Correlation of the reference is determined by digitalizing Figure 13 in Soroush et al.(2011).
P파 속도와 동탄성계수
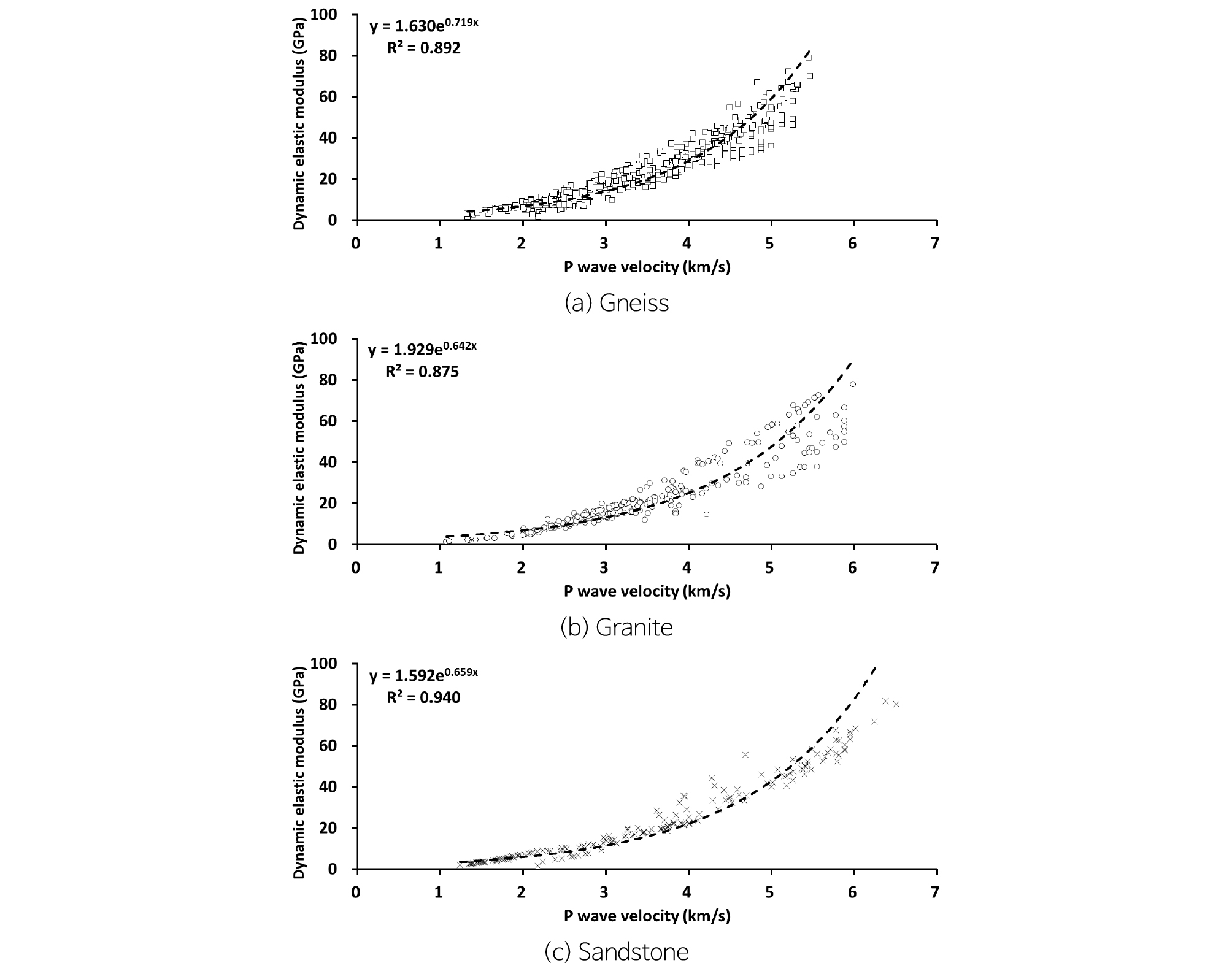
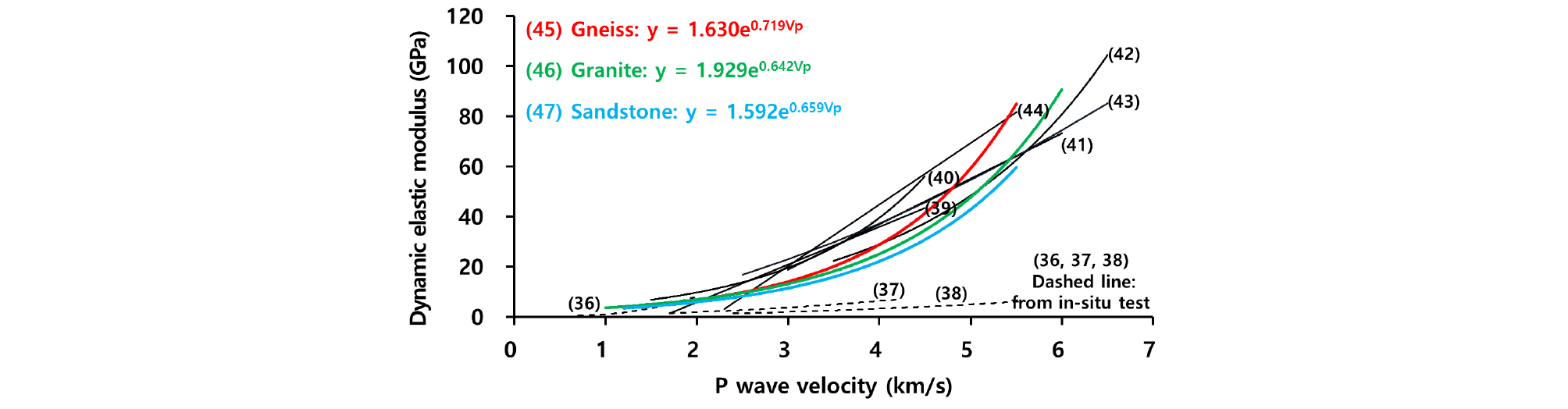
본 절에서는 암종별 P파 속도와 동탄성계수의 상관성을 분석하였다. 두 인자간의 상관관계는 지수함수의 형태로 결정계수는 0.875~0.940으로 높은 신뢰도를 보인다(Fig. 6). Table 3은 P파 속도와 동탄성계수의 상관관계에 대한 기존 문헌의 결과와 본 연구의 결과를 요약한 것이다. Fig. 7은 Table 3을 그래프로 도시화 한 것이다. 일부 연구자들은 P파 속도와 동탄성계수의 상관관계를 선형의 관계로 보고하고 있지만(Yale and Jamieson, 1994; Min et al., 2011), 다수의 연구자들은 지수함수의 형태로 제시하고 있다(Lee et al., 2008; Stan and Idziak, 2008; Sukplum et al., 2014). 동일한 시료를 이용하여 P파 속도와 정탄성계수, 그리고 정탄성계수와 동탄성계수의 관계를 이용하여 순차적으로 P파 속도와 동탄성계수의 상관관계를 도출하는 연구도 다수 수행되었다(modified from Christaras et al., 1994; Najibi et al., 2015; Chawre, 2018). 식 (41), (42), (43), (44)의 경우 P파 속도와 정탄성계수 및 정탄성계수와 동탄성계수의 식을 연립하여 P파 속도와 동탄성계수의 상관식을 도출하였다. 이 경우 도출된 상관식에 대한 신뢰도가 낮아질 수 있으나, 각각의 추정식이 0.870~0.988의 높은 결정계수를 가지고 있기 때문에 의미 있는 결과라고 할 수 있다.
Table 3. Relationship between the dynamic elastic modulus (Ed) and P wave velocity (Vp) proposed by previous studies and this study. All of the Ed values are in GPa
| References | Equation No. | Correlation | R2 | Rock type | Vp range (km/s) |
| Lee et al.(2008) | (36) | 0.911 | Granite | 0.7~2.0 | |
| Stan and Idziak(2008) | (37) | 0.900 | Sandstone, Basalt, Porphyry | 1.7~4.2 | |
| (38) | 0.770 | Limestone, Granite, Diabase | 2.4~5.6 | ||
| Min et al.(2011) | (39) | 0.974 | Granite | 1.7~4.5 | |
| Sukplum et al.(2014) | (40) | 0.952 | Clay, Silt, Sand-stone | 1.5~4.5 | |
| Yale and Jamieson(1994) | (41) | - | Carbonate | 3.0~6.0 | |
| Christaras et al.(1994)* | (42) | - | Various | 3.5~6.5 | |
| Najibi et al.(2015)* | (43) | - | Limestone | 2.5~6.5 | |
| Chawre(2018)* | (44) | - | Schist | 2.3~5.5 | |
| This study | (45) | 0.892 | Gneiss | 1.3~5.5 | |
| (46) | 0.875 | Granite | 1.0~6.0 | ||
| (47) | 0.940 | Sandstone | 1.2~6.5 |
Fig. 7에서 낮은 값을 보이는 상관식 (36), (37), (38)는 현장시험 데이터로부터 추정된 상관식이며(Lee et al., 2008; Stan and Idziak, 2008), 실내시험 결과로 부터 추정한 식보다는 다소 낮은 값을 보인다. 화강암, 사암, 편마암을 대상으로 본 연구에서 제안한 P파 속도와 동탄성계수의 상관식은 기존 연구사례와 비교할 때 약간 낮은 값을 보이지만 유사한 경향을 보이며, 결정계수도 비교적 높게 나타나고 있다.
결 론
본 연구에서는 국내에서 수행된 1,646개의 실내 및 현장시험 결과를 이용하여 암종별 P파 속도, 정탄성계수, 동탄성계수의 상관성을 분석하여 상관식을 제시하였으며, 기존의 연구사례와 비교하여 분석의 신뢰성을 검증하였다.
(1) P파 속도와 정탄성계수의 상관성을 분석한 결과, 편마암은 선형적인 관계를 보이며, 화강암과 사암은 지수함수의 관계를 보인다. 이들의 결정계수는 0.491~0.642로 높은 편에 속하진 않지만, 기존 연구사례의 P파 속도와 정탄성계수의 상관성과 유사한 분포범위를 보인다.
(2) 정탄성계수와 동탄성계수의 상관성은 모든 암종에서 선형적인 관계를 보인다. 일반적으로 정탄성계수보다 동탄성계수가 큰 값을 보이는 현상은 본 연구의 사암 데이터에서 비교적 두드러지게 나타나고 있다. 그 이유는 암석 내 공극이나 균열의 분포가 동적특성보다 정적특성에 더 큰 영향을 미치기 때문으로 판단된다.
(3) 동탄성계수와 정탄성계수에 대한 상관식은 결정계수가 0.541~0.676으로 높은 편에 속하진 않지만 둘의 관계는 선형으로 뚜렷한 경향을 보여준다. 기존 연구사례 중 경암을 대상으로 한 연구 결과들과는 유사한 분포를 보이지만 셰일, 석회암, 이암, 탄산염암과 같은 비교적 강도가 낮은 연암들을 대상으로 한 연구결과들과는 차이를 보이고 있다.
(4) P파 속도와 동탄성계수의 상관식을 기존 연구사례와 비교하면 다른 연구자들의 결과와 큰 차이를 보이지 않고, 결정계수가 0.875~0.940으로 높기 때문에 유의한 결과로 판단된다.