서 론
관련 연구 동향
지반굴착 시 히빙 문제
흙막이 벽체 지반굴착 수치해석 모델
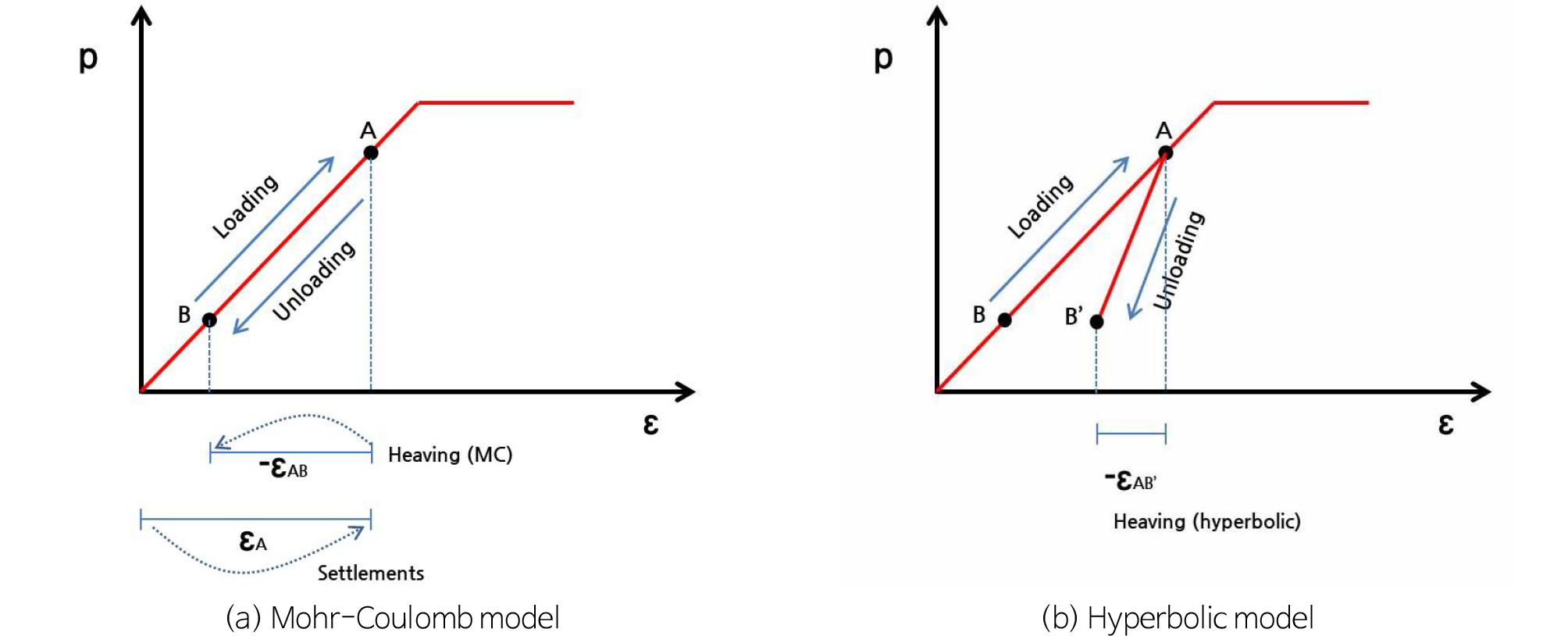
Mohr-Coulomb(MC) 모델
Hyperbolic 모델
수치해석 모델링
2차원 유한요소 수치해석
2차원 유한요소망 및 해석 단계
수치해석 매개변수
수치해석 결과 분석
최종 굴착 단계에 대한 지반 및 흙막이 벽체의 변위
굴착 단계 별 배면지반 연직침하
굴착바닥면에서의 연직응력
굴착바닥면에서의 수평응력
흙막이 벽체의 수평변위
결 론
서 론
최근 국내에서 지반함몰 현상이 최근 빈번하게 발생하는 추세이다. An et al.(2019)에 의하면, 지반함몰은 보통 지중매설관의 노후 및 접합 불량 등에 기인한 누수에 의해서 발생하거나, 터널 굴착 및 지하구조물 시공 시 잘못된 공법의 선택 또는 관리 부실로 인한 지하수의 유입으로 지하공동이 발생되어 일어난다고 제시하였다. 이러한 지반문제에 대한 국민 불안감 해소를 위해서 정부에서는 2018년 1월을 기점으로 지하안전관리에 관한 특별법을 시행하였다. 지난 2년 동안의 제도 시행에 따라서 많은 전문기관에서 지반굴착 시 안전영향에 대한 보고서 작성 및 평가 등의 과정을 통해서 경험을 축적 중이다. 하지만, 많은 시행착오를 겪고 있는 단계이기 때문에 많은 개선과 보완이 이루어져야 할 것으로 판단된다. 특히, 지반굴착공사 중 굴착지반의 거동 분석이 매우 중요하지만, 이에 대한 안정성 평가를 위한 절차가 세부적으로 제시되고 있지 않은 상황이다. 지반거동 문제는 크게 분류하면, 재하(loading) 문제와 제하(unloading) 문제로 대별할 수 있다. 지반굴착은 제하 문제이기 때문에 지반이 받고 있던 응력 상태가 해방되면서 발생하는 상황을 구현해야한다.
지반굴착에 의한 지반거동 해석은 필수적 요소 중 하나이다. 하지만, 지반굴착에 의한 안정성 평가 수행 중 수치해석적인 방법으로 접근 시 지반의 실제 거동을 잘 구현할 수 있는 지반모델이 존재함에도 불구하고, 사용의 편이성 등을 근거로 상대적으로 간편한 Mohr-Coulomb(MC) 모델이 많이 사용되고 있다. 재하 문제, 사면안정성 검토 등의 측면에서는 MC 모델의 수많은 축적된 자료, 사용성 편이 및 안전측 설계 등의 장점이 있지만, 지반굴착 문제에 대해서는 심각한 설계 오류가 발생할 문제가 있으므로 사용에 주의가 필요할 것으로 판단된다.
본 연구는 2차원 FEM 프로그램 PLAXIS 2D(Brinkgreve et al., 2016)를 사용하여 Hyperbolic 모델 중 대표적인 Hardening Soil(HS)과 MC 모델에 대해서 지반굴착 문제를 비교하였다. 국내에서 MC 모델 사용 시 지반융기 문제를 해결하기 위해서 많이 사용되고 있는 특별한 경계조건에 대해서도 적용하여 HS 모델의 결과와 비교하였다.
관련 연구 동향
수치해석 기반의 지반굴착 문제에 대해서 다양한 연구가 수행되었다. Yoo et al.(2010)은 흙막이 굴착 시스템의 거동에 대해서 수치해석적인 연구를 수행하였다. 강관 버팀보의 구조적 안정성을 흙막이 굴착 지반의 거동과 연계하여 새로운 시스템을 제안하였다. Choi and Yoo(2011)는 흙막이 굴착공사 시 지하수 저하에 의한 주변 지반의 공학적 거동을 수치해석 기반으로 수행하였다. 응력-간극수압의 연계 해석을 통한 지반변형범위를 제안하였다. Seong et al.(2011)은 수치해석기법을 사용하여 국내 대표적인 지반조건 및 공사공법에 따른 굴착 시 영향 분석을 수행하였다. 지반굴착 시 붕괴에 결정적 역할을 하는 요인 중에 하나로 보일링, 히빙 등 굴착 바닥면의 불안정을 제시하였다. Han et al.(2016)은 굴착안정성에 미치는 영향인자에 관한 분석을 수행하였다. 지반굴착에 따른 침투해석, 응력-변형 해석 등을 수치해석 기법을 사용하여 연구하였다.
또한, 지반 구성모델에 대한 비교연구도 많은 연구자들에 의해서 진행되었다. Hsieh and Ou(1997)은 점성토에 대해서 초기 재하 및 제하, 재재하(re-loading)를 고려한 hyperbolic 모델의 적용성을 비교하는 연구를 수행하였다. 이 연구에서는 지반굴착 시 융기량에 대한 검토가 이루어졌으며, 개선된 hyperbolic 모델을 사용할 것을 제안하였다. Obrzud(2010)은 지반 비선형 문제에 대해서 HS 모델을 적용한 수치해석에 관한 연구를 수행하였다. HS 모델이 지반굴착, 터널굴착 등 제하 문제에 적합성이 있다고 제안하였다. Yong and Oh(2016)는 사용이 간편하고, 경험적 상관관계에 의해서 간단하게 입력 물성치를 결정할 수 있어서 MC 모델이 지반굴착문제에 많이 사용되고 있지만, 깊은 굴착 문제에서는 MC 모델이 한계점을 보인다고 제시하였다. 이러한 한계점을 극복하기 위해서는 비선형 제하 문제에 적합한 HS 모델을 사용해야 한다고 제안하였다. Celik(2017)은 터널 공사 중 지표침하 문제에 대해서 MC 모델과 HS 모델을 비교하는 연구를 수행하였다. MC 모델은 응력수준 변화에 따른 수치해석에서 실제 거동과는 다른 결과가 산정된다고 제시하였다.
본 연구에서는 국내 지하안전영향평가 수행 시 많이 사용되고 있는 특별한 경계조건을 적용한 MC 모델을 제하 문제에 사용한 경우의 한계점을 분석하고, HS 모델을 적용해서 실제 지반굴착 시 공학적 거동에 대한 연구를 수행하였다.
지반굴착 시 히빙 문제
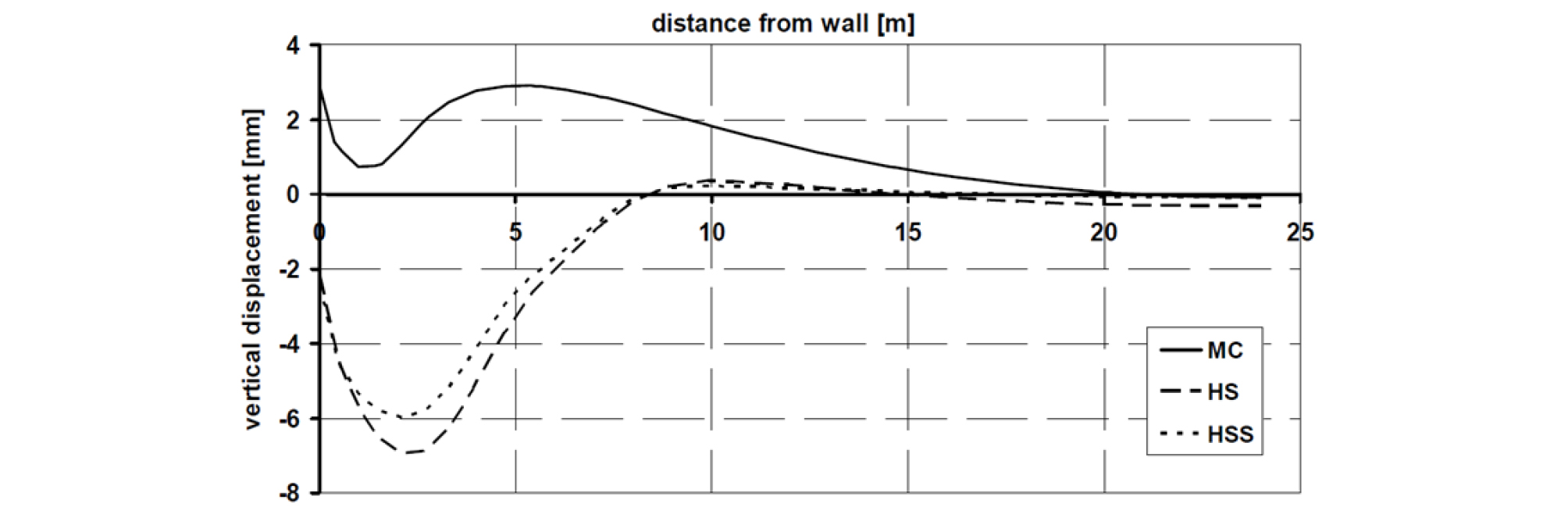
서론에서 언급한 바와 같이, 국내에서 지반굴착 시 공학적 거동 평가에 일반적으로 사용되고 있는 수치해석 지반모델은 MC 모델이다. 하지만 MC 모델을 사용해서 지반굴착 수치해석을 수행하면 실제 굴착면 융기량보다 과다한 히빙 현상이 발생하는 문제가 있다. Schweiger(2009)의 연구에 의하면, 상대적으로 깊은 굴착 현장에서는 MC 모델 대신 HS 모델을 사용해야한다고 제안하였다. Fig. 1에서는 MC 모델, HS 모델 및 HSS(hardening soil model with small strain) 모델에 대한 벽체 배면의 지표 침하량에 대한 수치해석 결과의 차이를 보여주고 있다.
Fig. 2에서는 제하 시 MC 모델을 사용하는 경우의 수치해석 결과와 실제 융기량과의 차이를 보여주고 있다. 국내 지반굴착에 관련한 수치해석 문제(특히, 지하안전영향평가 시)에 일반적으로 MC 모델을 많이 사용하고 있고, MC 모델의 과다한 히빙 현상을 제어하기 위해서 몇 가지 특별한 경계조건을 적용하여 이를 설계에 반영하고 있다. 여기서는 대표적인 2가지 케이스에 대해서 기술하였다. Fig. 3에서 보는 바와 같이, 실제 지반굴착 거동과는 전혀 상관없이 융기량 제어 목적으로 굴착바닥면에 굴착토 하중을 가하거나, 굴착바닥면에 연직 변위가 발생하지 않도록 변위를 고정하는 방법을 사용하고 있다.
Fig. 4에서는 수치해석에 적용된 지반모델 별 응력-변위 곡선을 보여주고 있다. 재하 시 침하거동과 제하 및 재재하 시 융기거동은 서로 다를 수밖에 없다. MC 모델에서는 이와 같은 응력-변위 곡선을 고려하기 어렵기 때문에 Duncan and Chang(1970)은 이러한 재하-제하-재재하 거동을 합리적으로 예측할 수 있는 hyperbolic 모델을 제안하였다.
그러므로 본 연구에서는 특별한 경계조건을 사용하지 않은 MC 모델 및 HS 모델에 대해서 수치해석을 수행하였고, MC 모델에 대해서는 특별한 경계 조건을 적용한 경우에 대해서도 수치해석을 수행하여 비교하였다. 비교 결과를 통해서 합리적인 지반굴착 수치해석 모델링 방안을 제시하고자 한다.
흙막이 벽체 지반굴착 수치해석 모델
지반거동을 분석하는데 사용할 수 있는 많은 수치해석 구성모델이 있고, 그 중 일부는 특정 유형의 지반을 위해서 개발된 반면에 일반적인 모델은 거의 모든 유형의 지반에 대해서 적용성이 있다. 일반적으로 많이 사용되는 모델은 선형탄성완전소성모델(Mohr-coulomb model), 탄소성 모델(Cam-clay model, Hardening soil model, Small strain hardening soil model), 운동학적 경화 기반의 탄소성 모델(Elastic-plastic models with kinematic hardening) 등이 있다. 이러한 구성모델 중에서 MC 모델 및 HS 모델은 실무에서 설계자가 많이 사용하고 있으며, 아래에 세부 내용을 기술하였다.
Mohr-Coulomb(MC) 모델
선형탄성완전소성모델(Linear Elastic Perfectly Plastic Model) 중에 대표적인 지반 구성모델이 MC 모델이다. 이 모델은 지반거동을 근사적으로 예측하는데 사용할 수 있다. MC 모델의 선형탄성 영역은 Hooke의 법칙에 근간을 두며, 완전소성 영역은 Mohr-Coulomb 파괴규준에 근간을 두고 있다. 선형탄성완전소성 MC 모델의 입력 매개변수는 5개(단위중량(), 탄성계수(), 포아송비(), 점착력(), 내부마찰각())로 구성되어있다. 이 5개 매개변수는 대부분의 지반공학 설계자에게 익숙한 변수이며, 실내실험, 현장시험 및 경험적인 방법을 통해 결정할 수 있다.
Hyperbolic 모델
Fig. 5에서는 Hyperbolic 모델의 응력-변형률 곡선을 보여주고 있으며, 이와 관련된 방정식은 식 (1) 및 식 (2)에 나타내었다. 이때, Hyperbolic Soil 모델의 지반정수는 , , , , , , , 이다.
| $$-\varepsilon=\frac1{E_i}\frac q{1-q/q_a}$$ | (1) |
| (2) |
여기서,
: 축차응력
: 점착력
: 내부마찰각
: 변형계수
: 기준 구속압(100 kPa)
: 구속압이 100 kPa일 때 변형계수
: 강성지수(0.5~1.0)
: 제하 및 재재하시 포아송비(0.2)
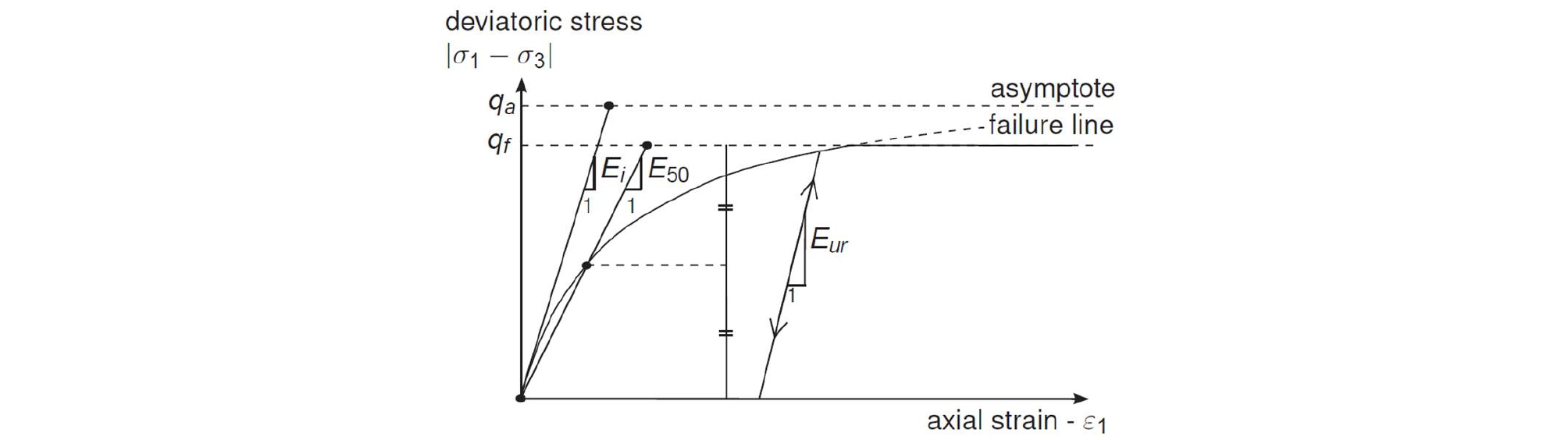
Fig. 5.
Hyperbolic stress-strain relation during primary loading in a standard drained triaxial test (Brinkgreve et al., 2016).
수치해석 모델링
2차원 유한요소 수치해석
Table 1에서는 본 연구에서 수행한 수치해석 케이스에 대해서 기술하였다. 지반 구성모델 별(MC, HS)과 굴착면 경계조건 별(굴착바닥면에 굴착토 하중을 적용, 굴착바닥면에 연직변위고정을 적용)에 따른 지반거동을 분석하기 위한 4가지 케이스의 2차원 유한요소해석을 수행하였다.
Table 1. Cases of numerical analysis
2차원 유한요소망 및 해석 단계
Fig. 6에서는 본 연구에서 이용된 2차원 유한요소망을 보여주고 있다. 기초지반은 매립층(0~3.0 m), 모래층(GL(-)3.0~ GL(-)90 m)으로 구성되어 있으며, 흙막이벽체는 지하연속벽, 지보재는 앵커(수평간격 2.5 m, 연직간격 3.0 m, 설치각도 33.7°)를 적용하였다. 지반 모델에 대해서는 매립층 및 모래층 모두 15절점 삼각형 요소로 격자망(mesh)을 구성하였고, HS 모델 또는 MC 모델을 적용하였다. 지하연속벽인 흙막이벽체는 Plate 요소를 적용하였고, Elastic 모델을 선택하였다. 앵커의 자유장은 Spring 요소를 적용하였고, Elastic 모델을 선택하였다. 앵커의 정착장은 Embedded Beam 요소와 Elastic 모델을 적용하였다. 흙막이벽체와 주변지반의 경계부는 두 재료의 강성 차이에 의한 미끄러짐 현상을 반영하기 위해서 Interface 요소를 적용하였으며, 지하수위에 대한 영향은 고려하지 않았다. 본 해석에 이용된 해석단계는 실제 시공 단계를 고려하기 위해서, 초기응력 재하, 지하연속벽 설치, 등분포 하중 활성화, 1단 굴착 및 1단 앵커 설치, 2단 굴착 및 2단 앵커 설치 ~ 9단 굴착 및 9단 앵커 설치, 10단 굴착의 순으로 수치해석 단계를 정의하였다.
수치해석 매개변수
본 연구에서 사용된 지반 모델에 대한 수치해석 매개변수는 Tables 2, 3에서 보여주고 있다. MC 모델의 매개변수는 실무에서 경험적으로 많이 사용되는 값을 적용하였으며, MC 모델에 적용한 값을 근거로 하여 식 (2)를 이용하여 HS 모델의 매개변수를 산정하였다. 또한, Tables 4, 5에서는 흙막이 벽체 및 앵커에 대해서 사용한 입력 매개변수를 보여주고 있다.
Table 2. MC model parameters
| Soil name | (kN/m3) | (kN/m2) | (kN/m2) | (°) | ||
| Upper soil layer | 16.0 | 500 | 0.35 | 1.0 | 30.0 | 0.5 |
| Lower soil layer | 17.0 | 30,000 | 0.3 | 1.0 | 34.0 | 0.5 |
Table 3. HS model parameters
| Soil name | (kN/m3) | (kN/m2) | (kN/m2) | (kN/m2) | (kN/m2) | (°) | ||
| Upper soil layer | 16.0 | 74,080 | 74,080 | 222,300 | 1.0 | 1.0 | 30.0 | 0.5 |
| Lower soil layer | 17.0 | 26,980 | 26,980 | 80,930 | 0.5 | 1.0 | 34.0 | 0.5 |
Table 4. Plate element parameters (wall)
| (kN/m2) | Diameter (m) | Interval (m) | (kN/m) | (kN) |
| 7.07 × 106 | 0.3 | 2.5 | 400 | 500,000 |
Table 5. Anchor element parameters
| Embedded Beam element (fixed area) | Spring element (free area) | ||||
| (kN/m2) | Diameter (m) | Interval (m) | (kN/m) | (kN) | Interval (m) |
| 7.07 × 106 | 0.3 | 2.5 | 400 | 500,000 | 2.5 |
수치해석 결과 분석
최종 굴착 단계에 대한 지반 및 흙막이 벽체의 변위
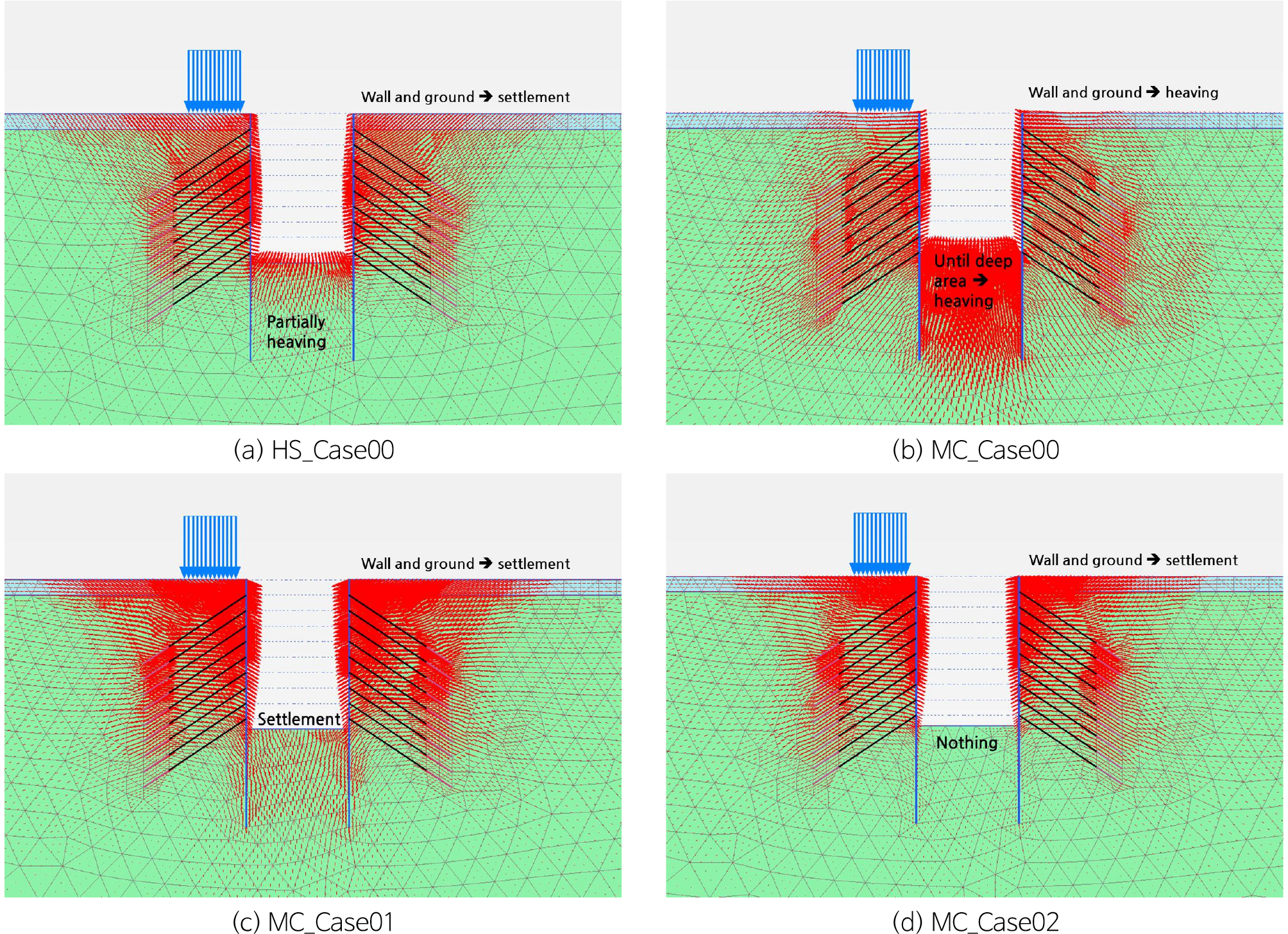
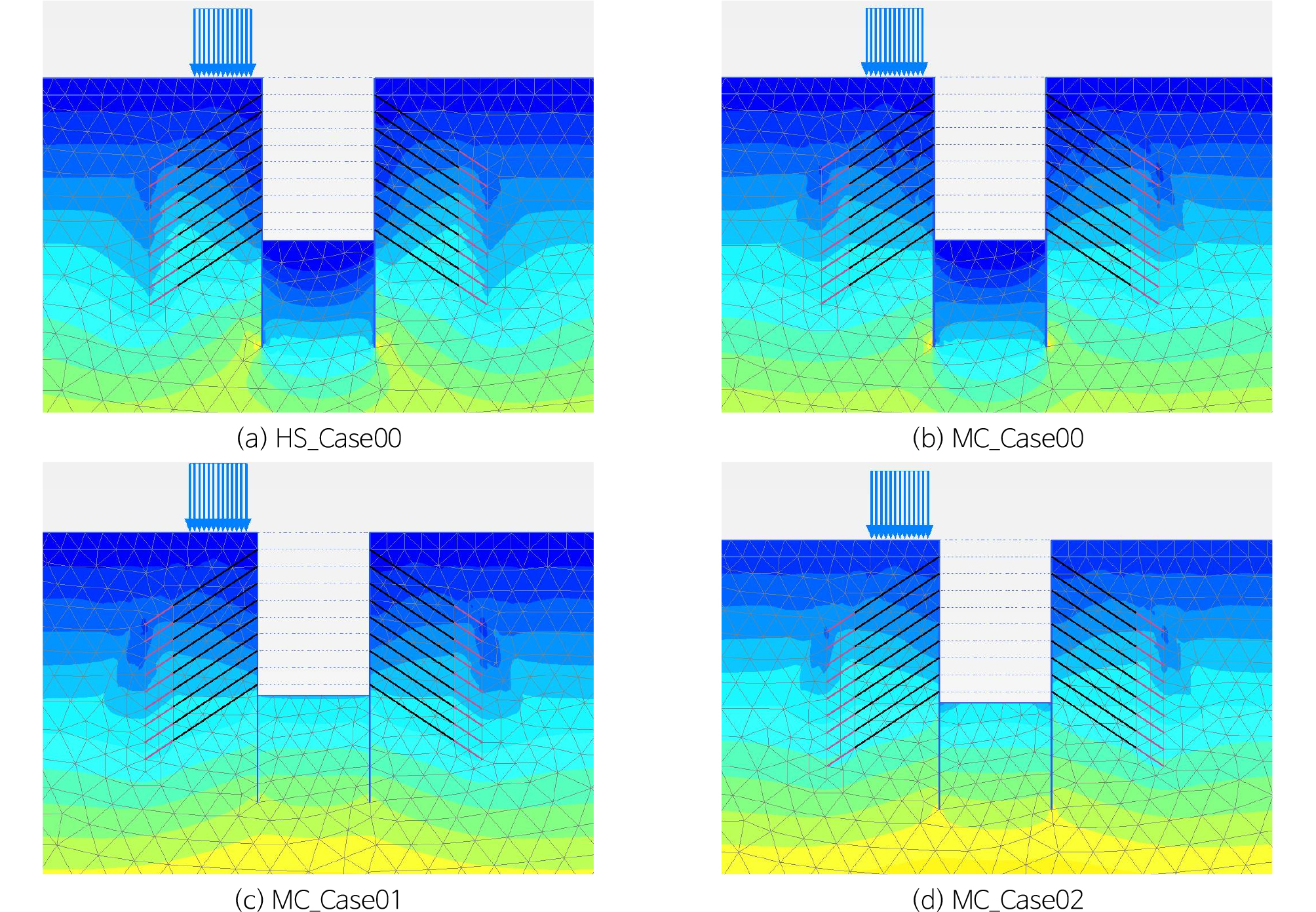
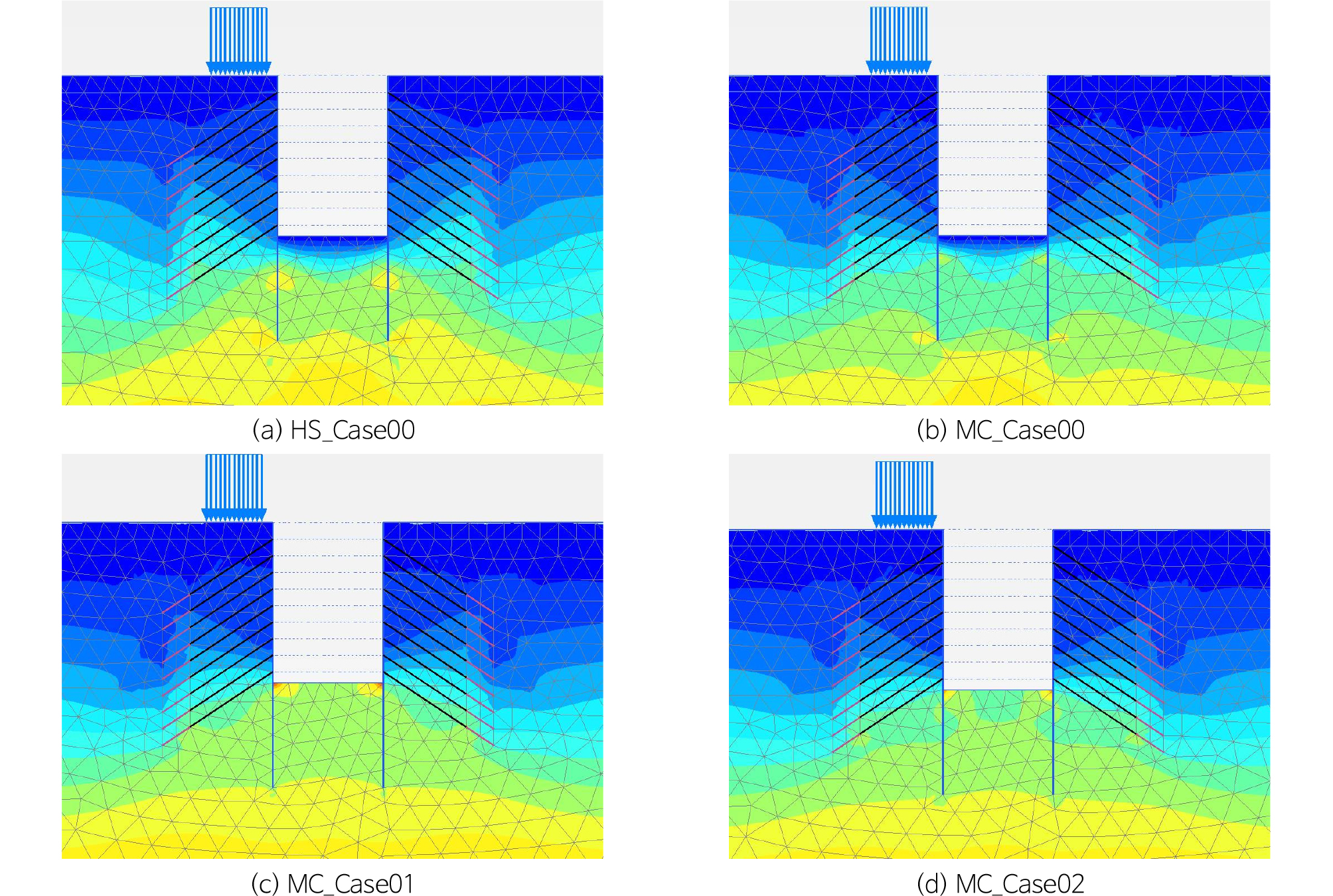
Fig. 7에서는 최종굴착 단계에서 변위벡터를 보여주고 있다. HS_Case00는 재하-제하-재재하 거동을 고려한 hyperbolic 모델을 수치해석에 적용한 경우이다. 이 경우에는 실제 지반거동과 유사한 결과를 보였다. 굴착면에서는 일부 융기가 발생하나, 흙막이벽체 및 배면지반에서는 융기가 발생하지 않고, 지반침하만 발생하고 있다. MC_Case00는 굴착면 깊은 심도까지 융기가 발생하며, 흙막이벽체 및 배면지반에서는 융기가 발생하고 있다. Mohr-Coulomb 모델을 지반굴착 문제에 적용하면 발생하는 한계점을 보여주고 있다. (b) 케이스에서 발생한 한계점을 극복하기 위한 방안이 아닌 굴착 바닥면의 융기량만을 억제하기 위한 방법으로 국내에서 일반적으로 사용되는 방법이 (c)와 (d)에 대한 경우이다. 굴착 바닥면에 굴착토 하중을 적용한 MC_Case01경우는 굴착바닥면, 흙막이벽체, 배면지반 모두 침하가 발생하고 있다. 굴착바닥면에 연직변위고정조건을 적용한 MC_Case02의 경우는 굴착바닥면에는 변위가 발생하지 않고 있으며, 흙막이벽체, 배면지반에는 침하가 발생하고 있다. 이러한 변위 발생 양상을 확인해보면, 굴착바닥면에서 일부 융기가 발생하고, 벽체 및 지반에서는 침하가 발생하는 양상을 보인 HS_Case00이 현실적인 지반 거동을 보여주고 있다고 판단된다.
굴착 단계 별 배면지반 연직침하
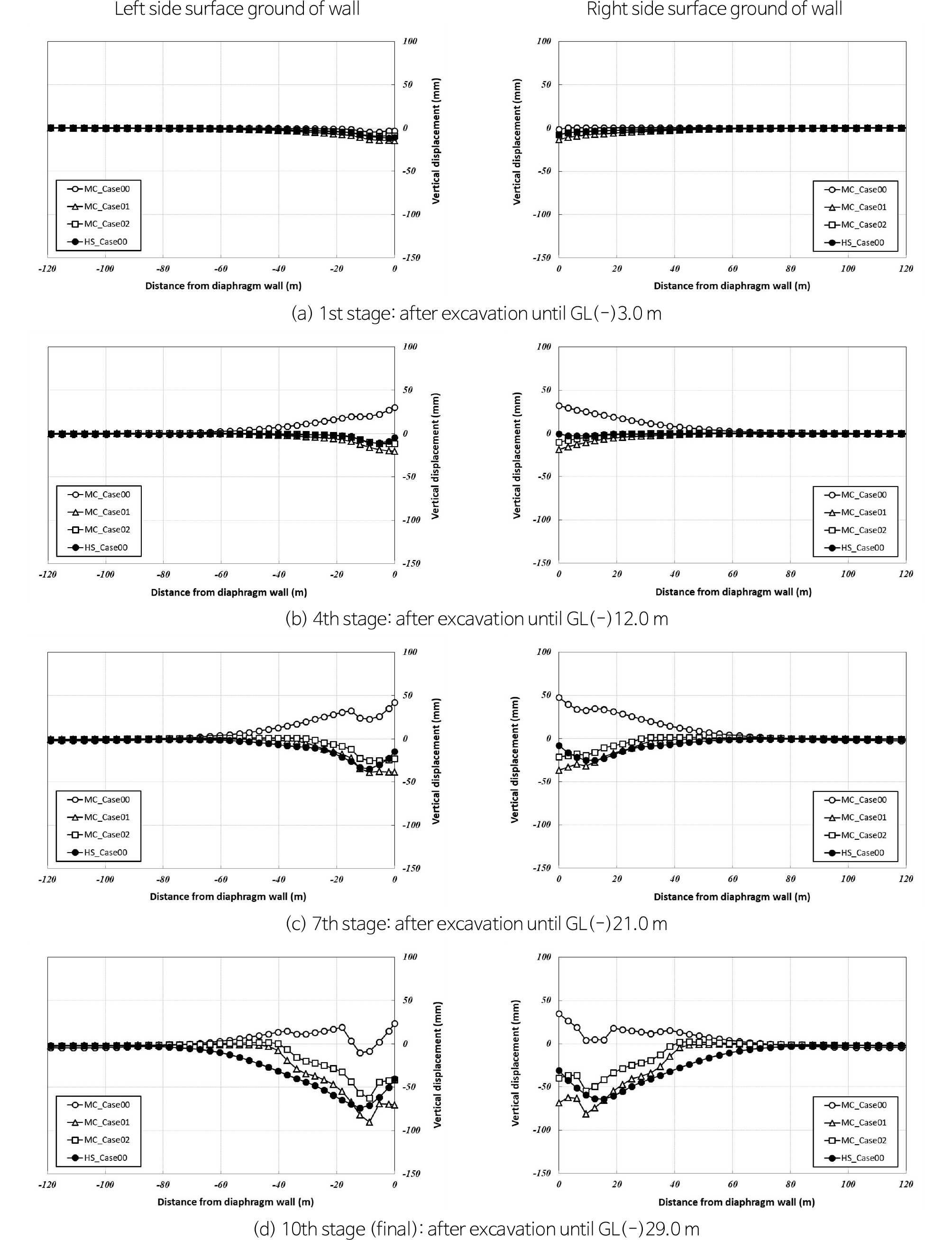
Fig. 8에서는 해석방법에 따른 지하연속벽 좌우측 배면지반의 굴착 단계 별 연직침하 발생 양상을 보여주고 있다. MC_Case00는 굴착 중 배면지반 융기가 크게 나타나고 있음을 알 수 있다. 일반적인 MC 모델은 배면지반 융기 거동에 맞지 않는 결과가 산정됨을 확인할 수 있다. 하지만, HS_Case00, MC_Case01 및 MC_Case02는 굴착 단계가 증가할수록 연직침하의 크기는 모두 유사하게 나타나고 있으나, 굴착에 의한 영향 범위는 HS_Case00가 약 70 m으로 MC_Case01와 MC_Case02 굴착영향범위(40 m)보다 크게 나타나고 있음을 확인할 수 있다.
굴착바닥면에서의 연직응력
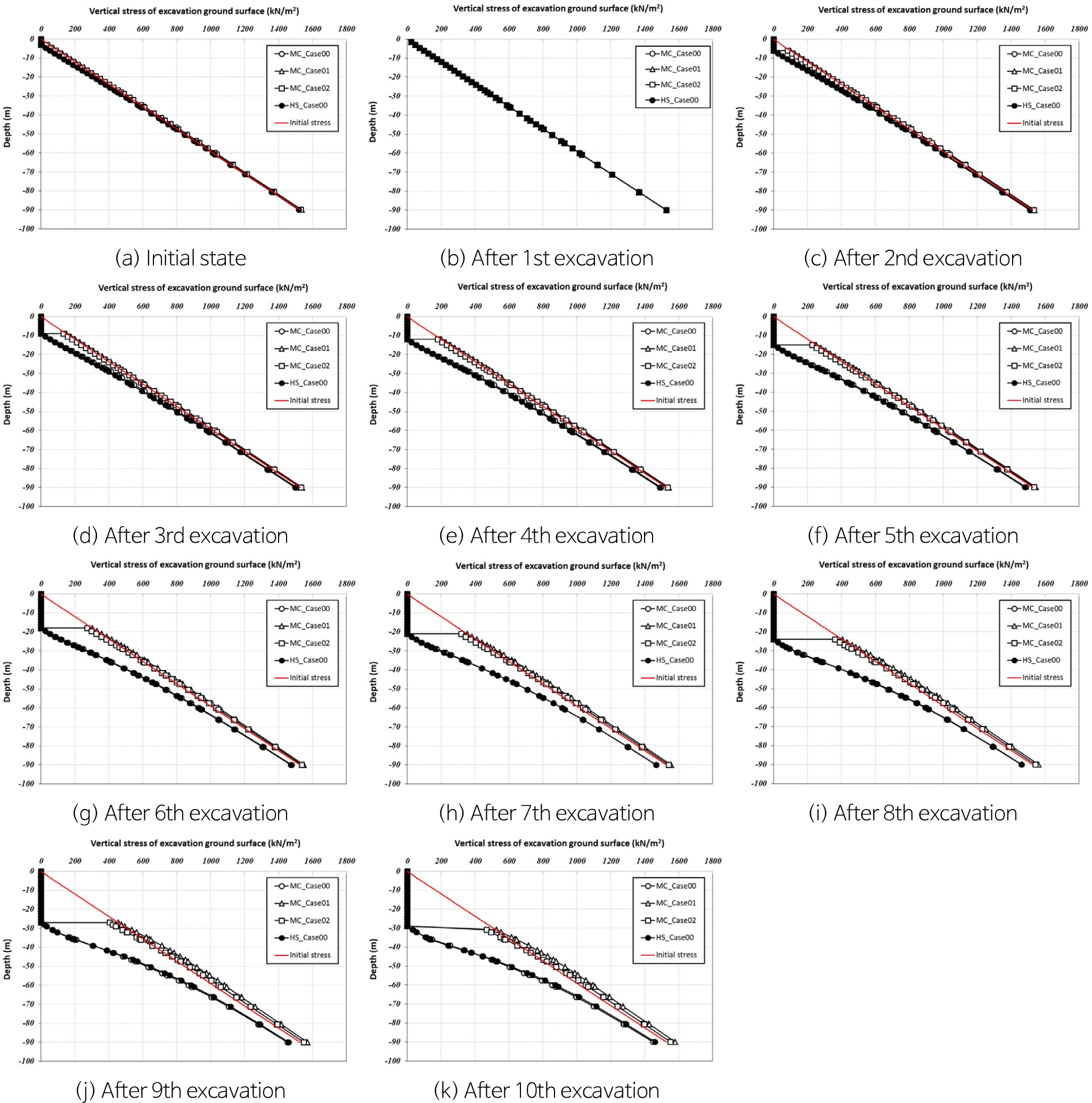
Fig. 9에서는 굴착단계 별 굴착바닥면에서부터 심도에 따른 연직응력의 변화 양상을 보여주고 있다. 굴착바닥면에 특별한 경계조건을 적용하지 않은 HS_Case00 및 MC_Case00의 경우에는 굴착바닥면에서 연직응력이 0.0 kN/m2이며, 굴착단계가 증가할수록 굴착바닥면 아래 지반에서의 연직응력이 감소하고 있음을 확인할 수 있다. 하지만, 굴착바닥면에 융기현상을 억제하기 위한 특별한 경계조건을 적용한 MC_Case01 및 MC_Case02는 굴착에 따른 연직응력의 변화는 없고, 초기연직응력과 동일하게 나타나는 경향을 보였다.
Fig. 10에서는 굴착단계 별 연직응력의 최종 굴착 단계에 대한 결과를 보여주고 있다. 이러한 결과에 의하여 굴착 바닥면에 실제 거동에 위배되는 특별한 경계조건을 적용해서 설계에 반영하는 배제해야 할 방법으로 판단된다.
굴착바닥면에서의 수평응력
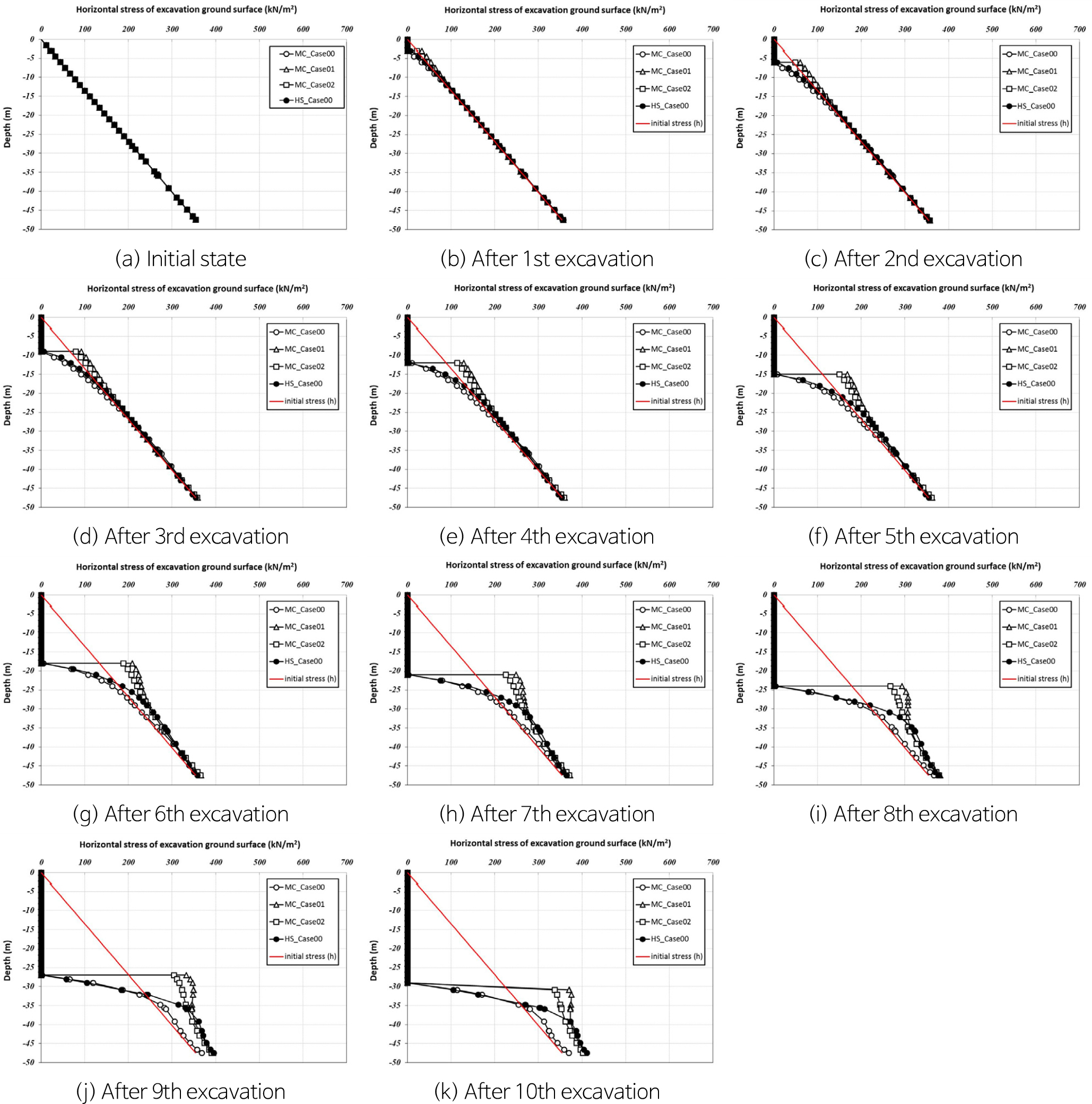
Figs. 11, 12에서는 굴착단계 별 굴착바닥면에서부터 심도에 따른 수평응력의 변화 양상을 보여주고 있다. 굴착바닥면에 특별한 경계조건을 적용하지 않은 HS_Case00 및 MC_Case00의 경우에는 굴착바닥면에서 수평응력이 0.0 kN/m2이며, HS_Case00에서는 굴착단계가 증가할수록 수평응력이 증가하는데, 이러한 결과는 굴착에 따른 흙막이 배면 토압의 증가 때문인 것으로 판단된다. 하지만, MC_Case00의 경우에서는 굴착단계가 증가하여도 수평응력의 변화가 발생하지 않는 결과가 산정되었다. 이러한 결과는 굴착면으로부터 깊은 심도까지 발생된 지반 융기 현상의 영향으로 판단된다. 특별한 경계조건이 적용된 MC_Case01 및 MC_Case02에서는 굴착면 바닥 부근에서의 수평응력이 매우 크게 나타나는 경향을 보였다.
흙막이 벽체의 수평변위
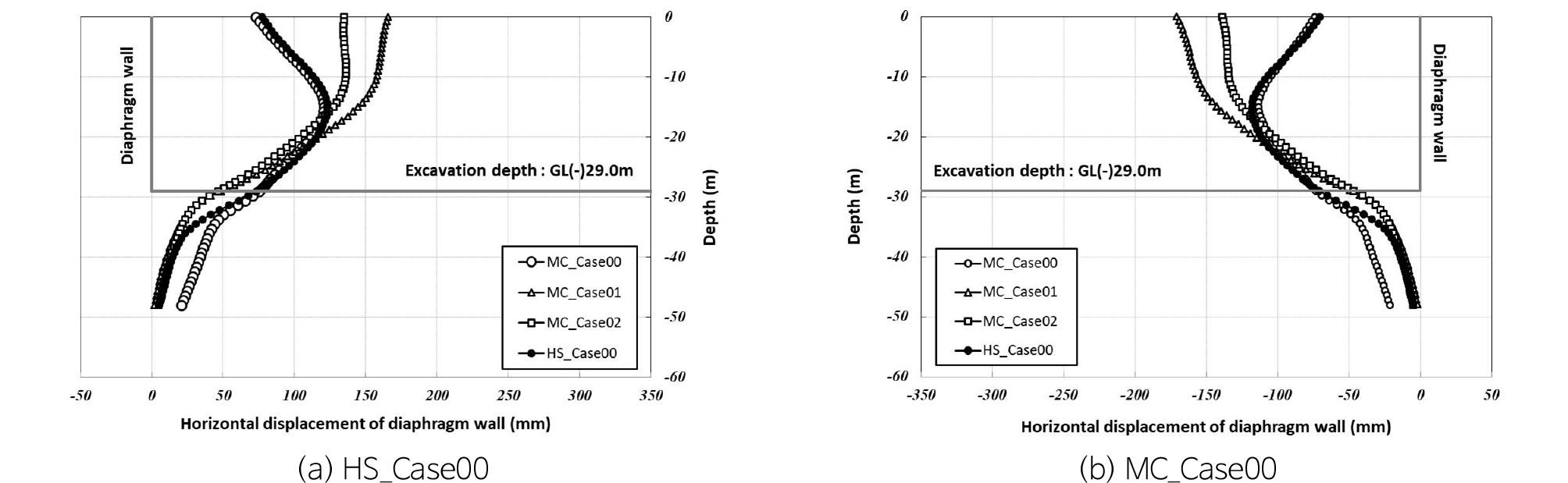
Fig. 13에서는 최종굴착 단계에서 흙막이 벽체의 수평변위를 보여주고 있다. 굴착바닥면에 특별한 경계조건을 적용한 경우에는 굴착바닥면에서 수평변위가 상대적으로 작게 발생하고, 흙막이 벽체 상단부에서 최대수평변위가 산정되었다. 굴착바닥면에 경계조건을 적용하지 않은 경우에는 흙막이 벽체 중간부에서 최대수평변위가 발생하는 것으로 산정되었다. 이러한 결과에 의해서 경계조건 적용여부에 따라 최대수평변위 발생위치가 다르게 산정됨을 확인할 수 있다.
결 론
본 연구에서는 지반굴착에 의한 지반거동 평가를 위해서 수치해석을 수행하였다. 기초지반에 대한 지반모델 별(Mohr- Coulomb, Hyperbolic) 및 굴착바닥면의 경계조건 별(굴착바닥면에 굴착토하중을 적용, 굴착바닥면에 연직변위고정을 적용)에 따른 2차원 유한요소해석을 수행한 결과에 의한 결론은 다음과 같다.
(1) 굴착바닥면에 굴착토하중을 적용한 경우(MC_Case01)에는 굴착바닥면에서 침하가 발생하고, 굴착바닥면에 연직변위를 고정한 경우(MC_Case02)에는 굴착으로 인한 연직거동이 발생하지 않으며, 특별한 경계조건을 적용하지 않은 경우(MC_Case00)에는 굴착면 하부 깊은 심도까지 융기와 흙막이벽체 및 지표면 융기가 발생하여 Mohr- Coulomb 모델을 적용할 경우에는 많은 한계점이 발생할 것으로 판단된다. 하지만 Hyperbolic 모델을 적용한 경우, 굴착바닥면에서의 약간의 융기가 발생하고, 흙막이벽체 및 지표면에서의 융기는 발생하지 않는 결과가 산정되어 실제 지반굴착에 의한 지반거동과 일치하는 것으로 판단된다.
(2) 굴착단계 별 연직침하 분석결과는 MC_Case00의 경우에는 과도한 지표융기가 발생하는 결과가 산정되었으며, HS_Case00, MC_Case01, MC_Case02의 최대 침하는 거의 유사하게 나타났으나, 침하영향범위는 HS_Case00가 70 m로 가장 크게 산정되는 결과를 보였다.
(3) 굴착면에서의 연직응력 및 수평응력을 분석결과를 확인해보면, 굴착바닥면에 특별한 경계조건을 적용한 MC_Case01, MC_Case02의 경우에는 굴착바닥면에서 연직 및 수평응력이 과도하게 발생하는 결과가 산정되었으나, HS_Case00 및 MC_Case00는 굴착바닥면에서의 연직 및 수평응력은 0으로 산정되었다. 따라서 굴착바닥면에 경계조건을 적용하지 않는 경우가 실제 지반거동과 일치하는 합리적인 모델링 방법이라 판단되고, 그 중에 Mohr-Coulomb 모델은 굴착바닥면 융기가 현실적이지 않기 때문에 Hyperbolic 모델을 사용하는 것이 합리적이라고 판단된다.